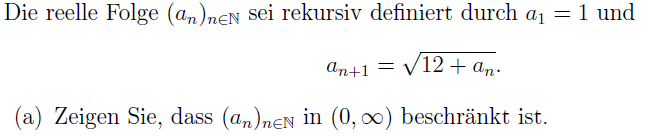
Problem/Ansatz:
Hallo zusammen,
ich habe jetzt als Lösung geschrieben,
dass (an) nach unten beschränkt ist, da
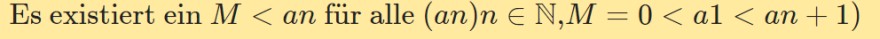
Text erkannt:
Es existiert ein \( M<a n \) für alle \( (a n) n \in \mathbb{N}, M=0<a 1<a n+1) \)
Text erkannt:
Es existiert ein \( M>a n \) für alle \( (a n) n \in \mathbb{N}, M=0<a 1<a n+1) \)
Dass es nach oben beschränkt habe ich so gezeigt:
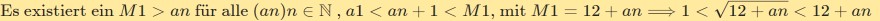
Text erkannt:
Es existiert ein \( M 1>a n \) für alle \( (a n) n \in \mathbb{N}, a 1<a n+1<M 1 \), mit \( M 1=12+a n \Longrightarrow 1<\sqrt{12+a n}<12+a n \)
Meine Frage ist, ob dies zulässig ist, trotz dessen, dass M1 nicht fest gewählt ist.
Vielen Dank.