Aufgabe:

Text erkannt:
Für \( i, j \in\{1, \ldots, n\} \) definieren wir die Matrizen \( E^{(i, j)} \in \mathrm{M}_{n \times n}(K) \) durch
\( E^{(i, j)}:=\left(e_{k, l}^{(i, j)}\right)_{\substack{1 \leq k \leq n \\ 1 \leq l \leq n}} \quad \text { mit } \quad e_{k, l}^{(i, j)}:=\left\{\begin{array}{ll} 1 & \text { falls } k=i \text { und } l=j, \\ 0 & \text { sonst. } \end{array}\right. \)
Für \( i \neq j \) und \( \lambda \in K \backslash\{0\} \) definieren wir damit die Elementarmatrizen in \( \mathrm{M}_{n \times n}(K) \) durch
\( \begin{aligned} S^{(i, j)} & :=\mathbf{1}_{n}-E^{(i, i)}-E^{(j, j)}+E^{(i, j)}+E^{(j, i)} \\ A_{\lambda}^{(i, j)} & :=\mathbf{1}_{n}+\lambda \cdot E^{(i, j)} \\ M_{\lambda}^{(i)} & :=\mathbf{1}_{n}+(\lambda-1) \cdot E^{(i, i)} \end{aligned} \)
(a) Sei zunächst \( K=\mathbb{Q} \) und \( n=3 \). Definiere
\( B:=\left(\begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array}\right) \in \mathrm{M}_{3 \times 3}(\mathbb{Q}) \)
Geben Sie die Matrizen \( S^{(2,3)}, A_{5}^{(1,3)} \) und \( M_{4}^{(2)} \) an und berechnen Sie für jede dieser Matrizen das Ergebnis der Multiplikation von rechts mit \( B \).
Problem/Ansatz:
2 Sachen:
1.
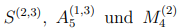
Text erkannt:
\( S^{(2,3)}, A_{5}^{(1,3)} \) und \( M_{4}^{(2)} \)
muss man logisch nur berechnen
das wären ja dann
S(2,3)=1_3 - E(2,2) - E(3,3) + E(2,3) + (3,2)
kann mir jemand bitte zeigen wie ich von dieser Schreibweise auf die Matrizenschreibweise komme?
2.
"berechnen Sie für jede dieser Matrizen das Ergebnis der Multiplikation von rechts mit B."
wegen dem von Rechts bin ich verwirrt
also
S*B
A*B
und M*B oder?
und ich bin mir unsicher, aber bei der multiplikation ist die Reihenfolge egal, welcher Matrix wo ist, also egal ob S*B oder B*S