Bestimmen Sie alle Häufungspunkte der Folge (zn) mit:

Question

Aufgabe:

Bestimmen Sie alle Häufungspunkte der Folge (zn) mit: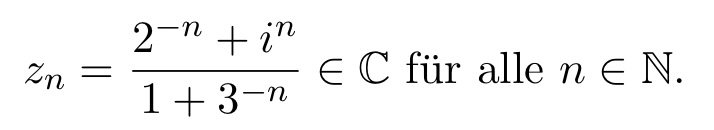

Text erkannt:

\( z_{n}=\frac{2^{-n}+i^{n}}{1+3^{-n}} \in \mathbb{C} \) für alle \( n \in \mathbb{N} \).

Begründen Sie, warum für diese Folge nicht lim inf und lim sup existieren.

Problem/Ansatz:

Hey ich komme bei der oben gestellten Aufgabe leider nicht weiter und würde mich über jede Hilfe freuen.

Answer 1

Betrachte die vier Teilfolgen

\((z_{4n}), \; (z_{4n+1}), \; (z_{4n+2}),\; (z_{4n+3})\).

Die Limiten dieser Teilfolgen sind die gesuchten Häufungspunkte.

Comments

Wie mache ich das?

---

\(i^{4n}, \; i^{4n+1}, \; i^{4n+2}\) und \(i^{4n+3}\) kannst du sicher

leicht ausrechnen. Der Rest dürfte dann kein Problem sein ...