Bestimmen Sie , falls existent ,alle kritischen Stellen

Question

Aufgabe: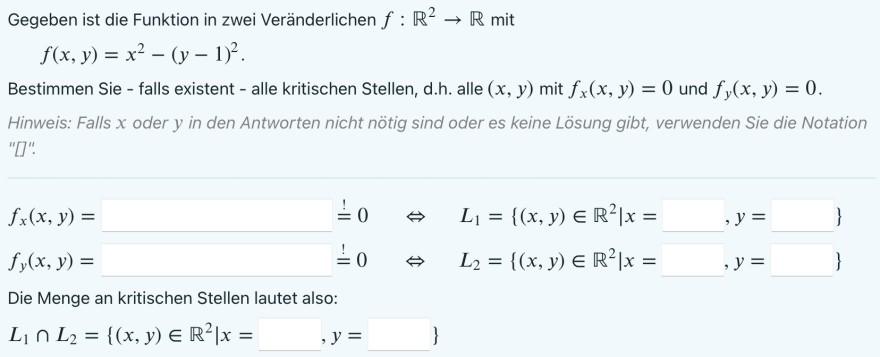

Text erkannt:

Gegeben ist die Funktion in zwei Veränderlichen \( f: \mathbb{R}^{2} \rightarrow \mathbb{R} \) mit
\( f(x, y)=x^{2}-(y-1)^{2} . \)
Bestimmen Sie - falls existent - alle kritischen Stellen, d.h. alle \( (x, y) \) mit \( f_{x}(x, y)=0 \) und \( f_{y}(x, y)=0 \).
Hinweis: Falls \( x \) oder \( y \) in den Antworten nicht nötig sind oder es keine Lösung gibt, verwenden Sie die Notation "[]".
\( \begin{array}{l} f_{x}(x, y)=\quad \stackrel{!}{=} 0 \quad \Leftrightarrow \quad L_{1}=\left\{(x, y) \in \mathbb{R}^{2} \mid x=\quad, y=\quad\right\} \\ f_{y}(x, y)=\quad \stackrel{!}{=} 0 \quad \Leftrightarrow \quad L_{2}=\left\{(x, y) \in \mathbb{R}^{2} \mid x=\quad, y=\quad\right\} \\ \end{array} \)
Die Menge an kritischen Stellen lautet also:
\( L_{1} \cap L_{2}=\left\{(x, y) \in \mathbb{R}^{2} \mid x=\quad, y=\quad\right\} \)

Problem/Ansatz: wie gehe ich hier voran ? mit Lösung bitte

Comments

Weißt du nicht, wie man eine partielle Ableitung
berechnet? Wenn das so ist, mach dich schleunigst schlau darin!

---

vgl:

https://www.mathelounge.de/366052/kritische-stellen-von-funktion-mit-zwei-variablen

Answer 1

Aloha :)

Die kritischen Stellen einer Funktion sind die Nullstellen des Gradienten.$$f(x;y)=x^2-(y-1)^2\implies\operatorname{grad}f(x;y)=\binom{2x}{-2(y-1)}\stackrel!=\binom{0}{0}$$Die Gleichung für die 1-te Koordinate lautet \((2x=0)\) und hat die Lösungsmenge:$$\mathbb L_1=\{(x;y)\in\mathbb R^2\,\big|\,x=0\;\land\;y=[]\}$$Die Gleichung für die 2-te Koordinate lautet \((2(y-1)=0)\) und hat die Lösungsmenge:$$\mathbb L_2=\{(x;y)\in\mathbb R^2\,\big|\,x=[]\;\land\;y=1\}$$Die Menge der kritischen Punkte lautet daher:$$\mathbb L_1\cap\mathbb L_2=\{(0;1)\}$$