Aufgabe:
Text erkannt:
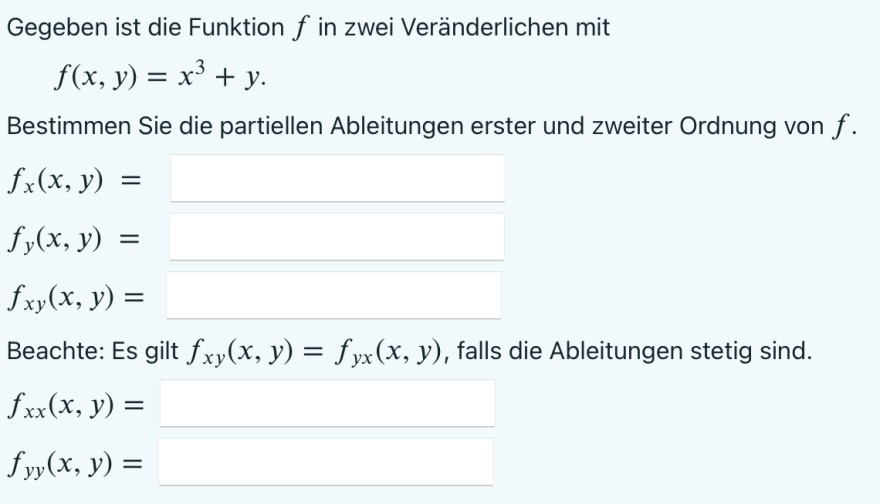
Gegeben ist die Funktion \( f \) in zwei Veränderlichen mit
\( f(x, y)=x^{3}+y . \)
Bestimmen Sie die partiellen Ableitungen erster und zweiter Ordnung von \( f \).
\( \begin{array}{l} f_{x}(x, y)= \\ f_{y}(x, y)= \\ f_{x y}(x, y)= \end{array} \)
Beachte: Es gilt \( f_{x y}(x, y)=f_{y x}(x, y) \), falls die Ableitungen stetig sind.
\( \begin{array}{l} f_{x x}(x, y)= \\ f_{y y}(x, y)= \end{array} \)
…
Problem/Ansatz: Brauche die Antworten ?