Wie berechnet man P(1<X<4) usw.?

Question

Aufgabe

Text erkannt:

Aufgabe 6: Gegeben ist folgende diskrete Wahrscheinlichkeitsfunktion:
\begin{tabular}{l|c|c|c|c}
\( x_{i} \) & 1 & 2 & 4 & 5 \\
\hline\( f_{X}\left(x_{i}\right) \) & \( \frac{1}{3} \) & \( \frac{1}{6} \) & \( \frac{1}{4} \) & \( \frac{1}{4} \)
\end{tabular}
a) Bestimmen Sie die Verteilungsfunktion.
b) Berechnen Sie \( P(0 \leq X<4), P(1 \leq X \leq 4), P(1<X<4), P(2<X \leq 5) \)

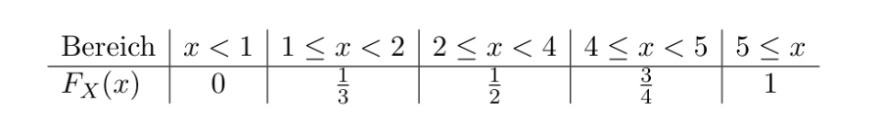
Text erkannt:

\begin{tabular}{l|c|c|c|c|c}
Bereich & \( x<1 \) & \( 1 \leq x<2 \) & \( 2 \leq x<4 \) & \( 4 \leq x<5 \) & \( 5 \leq x \) \\
\hline\( F_{X}(x) \) & 0 & \( \frac{1}{3} \) & \( \frac{1}{2} \) & \( \frac{3}{4} \) & 1
\end{tabular}

Problem/Ansatz

Wie bestimmt man nun die b) ?

Answer 1

P(1 ≤ X < 4) = P(X = 1) + P(X = 2) + P(X = 3)

P(1 ≤ X ≤ 4) = P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)

P(1 < X < 4) = P(X = 2) + P(X = 3)

P(2 < X ≤ 5) = P(X = 3) + P(X = 4) + P(X = 5)

wobei P(X = 3) = 0

Answer 2

Da in Teil (a) die Verteilungsfunktion bestimmt wurde, liegt es nahe, diese auch in Teil (b) zu benutzen:

$$P(0\leq X < 4) = F_X(2) = \frac 12$$$$P(1 \leq X \leq 4) = F_X(4) = \frac 34$$$$P(1 < X < 4) = F_X(2) - F_X(1) = \frac 16$$$$P(2 < X \leq 5) = F_X(5) - F_X(2) = \frac 12$$