Mathematica kompatibel:
9*8 + 7 + 6*54*3*2*1
12*3*(4 + 5)*6 + 7 + 8*9
1 + 2*3 + 4*567*8/9
17^2*7
Select[Range[1337, 2211, 7], Plus @@ IntegerDigits[#] == 7 &]
Ceiling[Csc[Cot[499/69]]*(Pi^Pi*Pi^Pi)]
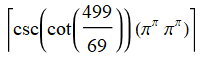
Floor[AppellF1[Pi, 1/Pi, 1/Pi, Pi, 1/Pi, 1/Pi^Pi]*1775]
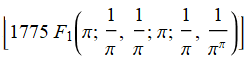
BaseForm[Prime[34], 4]
LinearRecurrence[{2, 0, -2, 1}, {0, 1, 7, 15}, 35] // Last
Last[Select[Range[3, 2100, 2],
CompositeQ[#] && Divisible[LucasL[# - (j = JacobiSymbol[#, 13]), 3] - 2*j, #] &]]
Last[FromDigits[IntegerDigits[#, 7]] & /@
Select[Range[800], CompositeQ[#] && PowerMod[7, # - 1, #] == 1 &]]
Die meisten Formeln können mit WolframAlpha.com nachgerechnet werden.