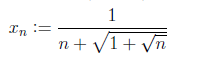
Text erkannt:
\( x_{n}:=\frac{1}{n+\sqrt{1+\sqrt{n}}} \)
Aufgabe: Es soll auf Konvergenz geprüft sowie der Grenzwert ermittelt werden.
Problem/Ansatz: zunächst gilt √1+√n > 0 sodass 0 < xn = 1/n+√1+√n
Dürfte soweit korrekt sein. Hat jemand einen Tipp für den Grenzwert? Vermute dass es sich um 0 handelt und die Folge konvergiert, weiß ab hier aber nicht weiter.