Aufgabe:
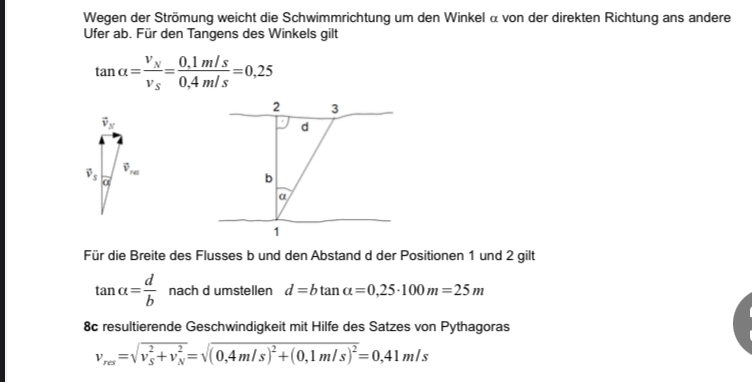
Text erkannt:
Wegen der Strömung weicht die Schwimmrichtung um den Winkel \( \alpha \) von der direkten Richtung ans andere Ufer ab. Für den Tangens des Winkels gilt
Für die Breite des Flusses \( b \) und den Abstand d der Positionen 1 und 2 gilt \( \tan \alpha=\frac{d}{b} \quad \) nach d umstellen \( \quad d=b \tan \alpha=0,25 \cdot 100 m=25 m \)
\( 8 c \) resultierende Geschwindigkeit mit Hilfe des Satzes von Pythagoras
\( v_{r o s}=\sqrt{v_{s}^{2}+v_{N}^{2}}=\sqrt{(0,4 \mathrm{~m} / \mathrm{s})^{2}+(0,1 \mathrm{~m} / \mathrm{s})^{2}}=0,41 \mathrm{~m} / \mathrm{s} \)
Problem/Ansatz:
Ich wollte fragen, was dir 0.25 sind ist das jetzt ein Meter oder ein Winkel? Denn es wurde 0.25* 100m (Länge von b) gerechnet. Ich verstehe nicht ob es eine bestimme Formel ist oder sonstiges.