Welchen maximalen Umfang kann das Rechteck besitzen? Optimierung

Question

Aufgabe:

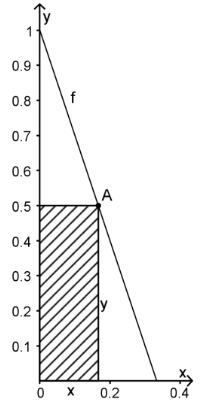
Die rechte obere Ecke eines Rechecks soll auf dem Graphen der Funktion f mit f(x)=-3x+1
liegen und die untere linke Ecke im Ursprung des Koordinatensystems.
Die Seiten des Rechtecks liegen auf bzw. parallel zu den Koordinatenachsen.

a) Welchen maximalen Umfang kann das Rechteck besitzen?

Problem/Ansatz:

Wie komme ich auf die Zielfunktion bzw. wie gehe ich hier vor?

Answer 1

Flächeninhalt des Rechtecks ist

        \(F = x\cdot y\).

Dabei liegt der Punkt \((x|y)\) auf dem Graphen von \(f\). Also ist

        \(y = f(x)\).

Somit ist

        \(F = x\cdot f(x)\).

Answer 2

Hallo,

die Zielfunktion ist der Flächeninhalt des Rechtecks.

Allgemein berechnest du ihn mit \(A_{\text{Rechteck}}=a\cdot b\).

Hierbei ist a = x und b = f(x).

Hilft dir das weiter?

Gruß, Silvia

Answer 3

Hallo,

a) Welchen maximalen Umfang kann das Rechteck besitzen?

0<x<⅓

u=2x+2y

y=-3x+1

--> u(x)=2x -6x +2 = -4x+2

u'(x)=-4≠0

Es kann nur ein Randmaximum geben.

u(0)=2

u(⅓)=⅔

Maximal wäre der Umfang bei x=0. Allerdings gehört x=0 nicht zur Definitionsmenge, sodass es kein Rechteck mit maximalem Umfang gibt.