rechtwinkliges Dreieck im Dreieck

Question

Aufgabe:

Gegeben ist das Dreieck ABC.

Es gilt:
\( \begin{array}{l} \overline{A B}=8,4 \mathrm{~cm} \\ \alpha=44,2^{\circ} \\ A_{A B C}=23,6 \mathrm{~cm}^{2} \end{array} \)
Berechne den Winkel \( \beta \) sowie den Abstand des Punktes D zur Strecke \( \overline{A B} \).

Problem/Ansatz:

Ich verstehe das thema gar nicht und weiß nicht wie ich anfangen soll sowas zu berechnen :(

Answer 1

Hallo,

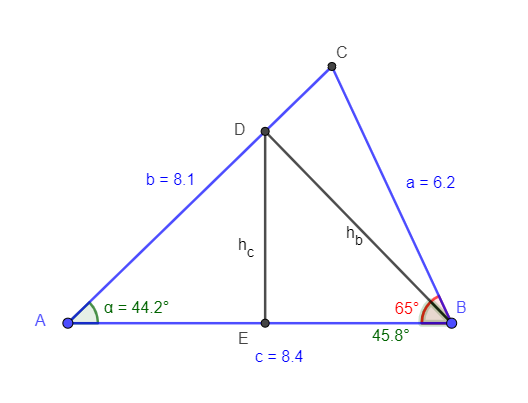
berechne zunächst die Strecke DB. Wende den Sinussatz an.

\(\overline{DB}=\frac{8,4\cdot \sin(44,2)}{\sin(90)}=5,8562\). sin(90°) kann man sich sparen, weil = 1, aber ich habe es der Vollständigkeit halber aufgeschrieben.

Du weißt \(\frac{\overline{AC}\cdot \overline{DB}}{2}=23,6\). Daraus ergibt sich \(\overline{AC}=b=8,06\).

Die Strecke \(\overline{BC}=a\) kannst du mit dem Kosinussatz berechnen.

\( a=\sqrt{b^{2}+c^{2}-2 \cdot b \cdot c \cdot \cos (\alpha)} =6,2\)

Den Winkel \(\beta\) kannst du beispielsweise wieder mit dem Sinussatz berechnen.

Der Abstand des Punktes D zu AB ist die Länge der Höhe \(h_c\). Betrachte hierzu zunächst das Dreieck ABD und dann ADE.


Ich gehe davon aus und hoffe, dass es weniger aufwendige Lösungen gibt.

Gruß, Silvia