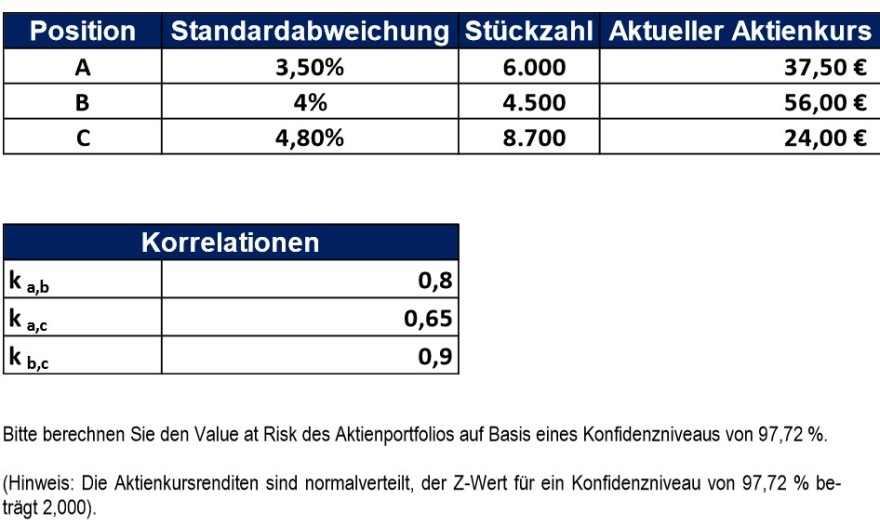
Hallo, bisher weiß ich nur wie man den VaR eines Portfolios bei 2 Aktienpositionen von z.B. A und B.
RMZ = Risikomesszahl = Standardabweichung * Konfidenzintervall
RMZ (A) = 3,5% * 2,0000 = 7%
RMZ (B) = 4% * 2,0000 = 8%
RV = Risikovolumen = Stückzahl * Preis
RV (A) = 6000 * 37,5€ = 225 000€
RV (B) 4500 * 56€ = 252 000€
VaR (A) = RMZ (A) * RV (A) = 7% * 225 000€ = 15 750€
VaR (B) = RMZ (B) * RV (B) = 8% * 252 000€ =20 160€
und nun würde man den VaR des Portfolios, wenn es nur aus A und B bestehen würde, so ausrechnen:
VaR (Portfolio) = \( \sqrt{VaR (A)² + VaR (B)² + 2 * VaR (A) * VaR (B) * Korrelationskoeffizient (A,B)} \)
bis hierhin ist mir auch alles klar.
Würde man es bei den 3 Aktienpositionen so machen, dass man erst
VaR (A,B)
VaR( A,C)
VaR (B,C)bestimmt und diese dann jeweils in die VaR (Portfolio) Formel mit dem dazugehörigen Korrelationskoeffizienten einsetzt?
Dann hat man 3 Ergebnisse und addiert diese auf.
Gibt es dafür vielleicht eine Formel, mit der man das direkt berechnen kann?