Komplexe Zahlen in Polardarstellung. Warum ist e^{jπ}= -1?

Question

warum ist  e^{jπ}=-1???

Ich kann dies leider nicht nachvollziehen

Könnte mir das mal jemand erklären? Danke schon im Voraus

Answer 1

 

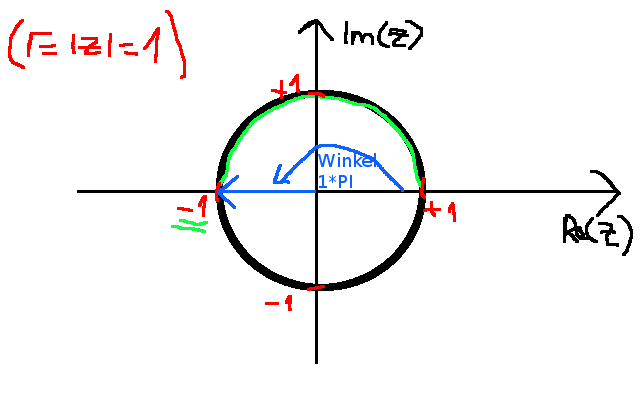
hier ist eine anschauliche Begründung, warum e^j*PI = -1 ist. Schau es dir einfach auf den Einheitskreis an, denn der Betrag von ej*PI ist 1, also der Radius ist 1. D.h der Umfang des Kreises ist

2*PI

Jetzt heißt ja der Winkel PI, dass man 180 Grad gegen den Uhrzeigersinn im Einheitskreis gehen soll. (Weil der Winkel positiv ist, wäre er negativ, müsste man MIT den Uhrzeigersinn gehen)

 

Du kannst jede reelle negative Zahl als komplexe Zahl in der eulerschen Form schreiben, indem du das Minuszeichen entfernst und stattdessen "* e^j*pi" an anhängst.

Jede reelle positive Zahl kann als komplexe Zahl in der eulerschen Form geschrieben werden, indem man an diese Zahl einfach "*e^j*0" anhängt. Und da e^j*0 = 1 ist (Winkel ist 0 Grad), stimmt die Aussage.

Answer 2

Das ist die Definition der Komplexen Zahlen in Polarform

a * e^{phi * i}

Bedeutet eine Komplexe Zahl mit dem Betrag a der einen Winkel von phi mit der Positiven x-Achse einschließt

1 * e^{pi * i}

ist also die Komplexe Zahl die den Betrag 1 hat und einen Winkel von pi = 180° mit der positiven x-Achse einschließt.

Damit ist es genau eine Einheit in Richtung negativer x-Achse also -1.