Was bedeutet 'lim' in der Mathematik? Und wann schreibt man das?

Question

Bei manchen Aufgaben sehe ich, dass da steht: Lim x→∞ aber was heißt das? Und wofür steht das?

Wann schreibt man das? Kann man das ausrechnen? 

\( \lim \limits_{x \rightarrow+\infty} f(x) \) bzw. \( \lim \limits_{x \rightarrow-\infty} f(x) \)

Answer 1

Hi Emre,

wenn Du eine Funktion im unendlichen untersuchen willst (also wissen, was mit der Funktion passiert, wenn Du ganz weit rechts oder links bist), dann wird das mit dem "Grenzwert", also der Limesschreibweise verdeutlicht :).

Das kann man natürlich ausrechne/abschätzen.

 

Für f(x) = 1/x

Kannst Du zum Beispiel sagen "Wenn der Nenner ganz groß wird, dann geht f(x) selbst gegen 0". Nichts anderes beschreibt

$$\lim_{x\to \infty} \frac1x = 0$$

Beachte, dass "Grenzwert" bedeutet, dass der Wert nie erreicht wird, sondern nur sich "anschmiegt" ;).

 

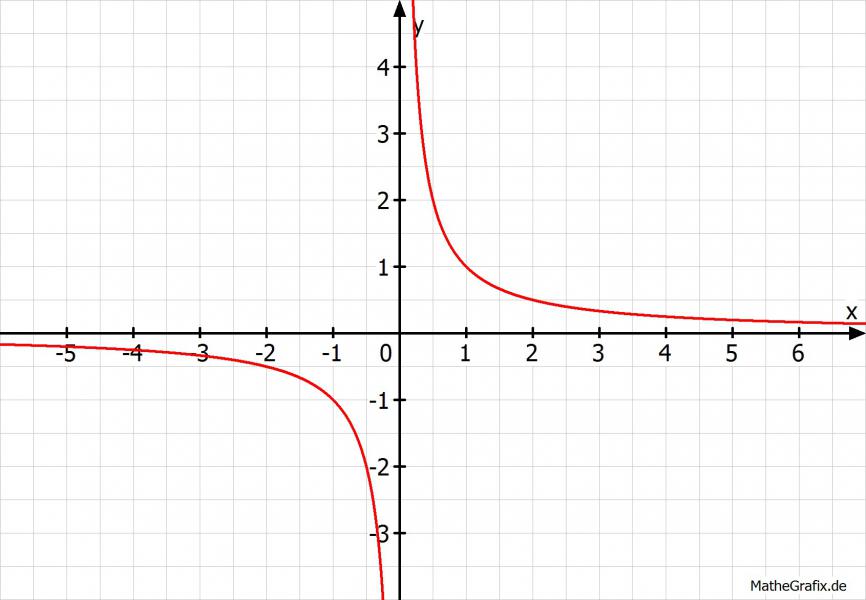
Das sieht man auch im Schaubild:

 

 

Grüße

Answer 2

Normal darf man in f(x) für das x ja nur reelle Zahlen aus R einsetzen. Unendlich (∞) ist keine Zahl die eingesetzt werden kann. aus diesem Grund bildet man den Grenzwert lim (x → ∞). Das heißt man tut so als fürde man etwas unendliches einsetzen und versucht dann zu bestimmen was dabei heraus kommt. Dabei gilt dann z.B.

lim (x → ∞) x = ∞

Das heißt wenn ich für x unendlich einsetze kommt auch unendlich raus.

lim (x → ∞) 1/x = 0

Wenn ich bei 1/x für x unendlich einsetze teile ich quasi durch unendlich und dann kommt näherungsweise 0 heraus. 0 ist ein Grenzwert. Exakt 0 wird selber bei der Rechnung nicht heraus kommen. aber 0 ist eine Grenze an denen sich der Wert für größer werdende x annähert.