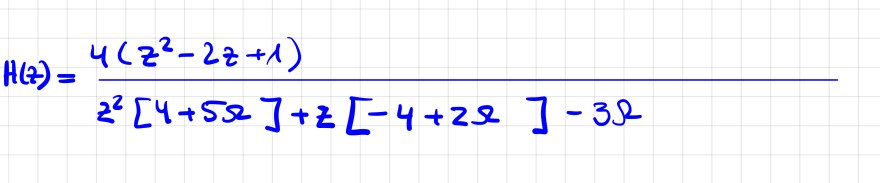Aufgabe:
Gegeben ist folgende Funktion:
\( H(s)=\frac{\frac{1}{\omega_{g}^{2}} \cdot s^{2}}{\frac{1}{\omega_{g}^{2}} \cdot s^{2}+\frac{2}{\omega_{g}} \cdot s+1} \).
Für s soll folgendes eingesetzt werden: \( s=\frac{2}{T} \cdot \frac{z-1}{z+1} \)
Zur Vereinfachung gilt: w * T = Ω
Am Ende soll dies in die Form umgeschrieben werden:
\( H(z)=\frac{a_{0}+a_{1} \cdot z^{-1}+a_{2} \cdot z^{-2}}{1+b_{1} \cdot z^{-1}+b_{2} \cdot z^{-2}} \)
Könnte jemand bitte einmal die komplette Rechnung zeigen. Damit ich es mit meinen abgleichen kann. Wäre eine sehr interessante und wichtige Aufgabe für mich.
Meine Lösung:
Ich bin zwar noch nicht fertig mit der Auflösung mit z^2 zu dividieren. Aber ich möchte gerne zumindestens wissen ob das so richtig ist?