Aufgabe:
Folgengrenzwerte
Problem/Ansatz:
Folgengrenzwerte
Sei 0 ≤ q ≤ 1 und
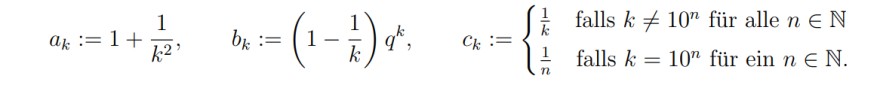
Text erkannt:
\( a_{k}:=1+\frac{1}{k^{2}}, \quad b_{k}:=\left(1-\frac{1}{k}\right) q^{k}, \quad c_{k}:=\left\{\begin{array}{ll}\frac{1}{k} & \text { falls } k \neq 10^{n} \text { für alle } n \in \mathbb{N} \\ \frac{1}{n} & \text { falls } k=10^{n} \text { für ein } n \in \mathbb{N} .\end{array}\right. \)
Erraten Sie die Grenzwerte der Folgen (ak)k∈N, (bk)k∈N und (ck)k∈N und beweisen Sie die
Konvergenz.
// Kommentar;
Ich denke, bei ak und bk ist zu beachten, dass 1/k2, 1/k und qk kleiner werden, wenn k größer wird (es sei denn, q=1, man muss dort eine Fallunterscheidung treffen), das sollte helfen, die Grenze zu erraten. Ich dachte, ich kann für ck im zweiten Fall n=log10(k) einsetzen und dann k ≥ log10(k) verwenden, um zu finden;
0≤ck≤ 1/ log10(k)
Aber ich wusste nicht, was ich für die Antwort weiter tun sollte. Ich freue mich, wenn Sie helfen.
LG