Wie berechnet man die darstellende Matrix von MEB(f) von f bez. B und E

Question

Aufgabe:

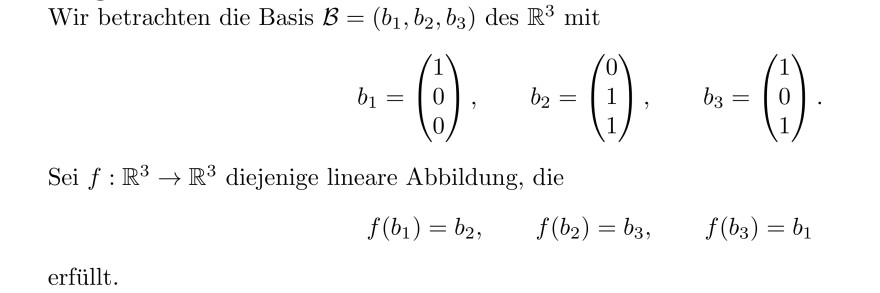
Text erkannt:

Wir betrachten die Basis \( \mathcal{B}=\left(b_{1}, b_{2}, b_{3}\right) \) des \( \mathbb{R}^{3} \) mit
\( b_{1}=\left(\begin{array}{l} 1 \\ 0 \\ 0 \end{array}\right), \quad b_{2}=\left(\begin{array}{l} 0 \\ 1 \\ 1 \end{array}\right), \quad b_{3}=\left(\begin{array}{l} 1 \\ 0 \\ 1 \end{array}\right) . \)
Sei \( f: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3} \) diejenige lineare Abbildung, die
\( f\left(b_{1}\right)=b_{2}, \quad f\left(b_{2}\right)=b_{3}, \quad f\left(b_{3}\right)=b_{1} \)
erfüllt.

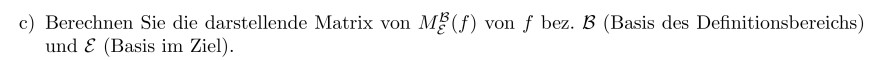
Text erkannt:

c) Berechnen Sie die darstellende Matrix von \( M_{\mathcal{E}}^{\mathcal{B}}(f) \) von \( f \) bez. \( \mathcal{B} \) (Basis des Definitionsbereichs) und \( \mathcal{E} \) (Basis im Ziel).

Problem/Ansatz:

Wie verstehe ich Basis des Definitionsbereich und Basis im Ziel. Verstehe nicht, wie ich die Aufgabe lösen kann.

Answer 1

Aloha :)

Willkommen in der Mathelounge... \o/

Du kennst die Abbildungsmatrix für Eingangsvektoren bezüglich der Basis \(B\) und Ausgangsvektoren bezüglich der Basis \(B\):$$f(\vec b_1)=\vec b_2\;;\;f(\vec b_2)=\vec b_3\;;\;f(\vec b_3)=\vec b_1\quad\implies\quad M^{B}_B=\left(\begin{array}{rrr}0 & 0 & 1\\1 & 0 & 0\\0 & 1 & 0\end{array}\right)$$Da die Koordinaten der Basisvektoren \(\vec b_i\) von \(B\) bezüglich der Standardbasis \(E\) angegeben sind, kennst du auch die Transformationsmatrix von \(B\) nach \(E\):$$\operatorname{id}^B_E=\left(\begin{array}{rrr}1 & 0 & 1\\0 & 1 & 0\\0 & 1 & 1\end{array}\right)$$Damit kannst du die Ausgangsvektoren von \(M^B_B\) in die Basis \(E\) transformieren:$$M^B_E=\operatorname{id}^B_E\cdot M_B^B=\left(\begin{array}{rrr}1 & 0 & 1\\0 & 1 & 0\\0 & 1 & 1\end{array}\right)\left(\begin{array}{rrr}0 & 0 & 1\\1 & 0 & 0\\0 & 1 & 0\end{array}\right)=\left(\begin{array}{rrr}0 & 1 & 1\\1 & 0 & 0\\1 & 1 & 0\end{array}\right)$$

Comments

Vielen lieben Dank für die Hilfe!