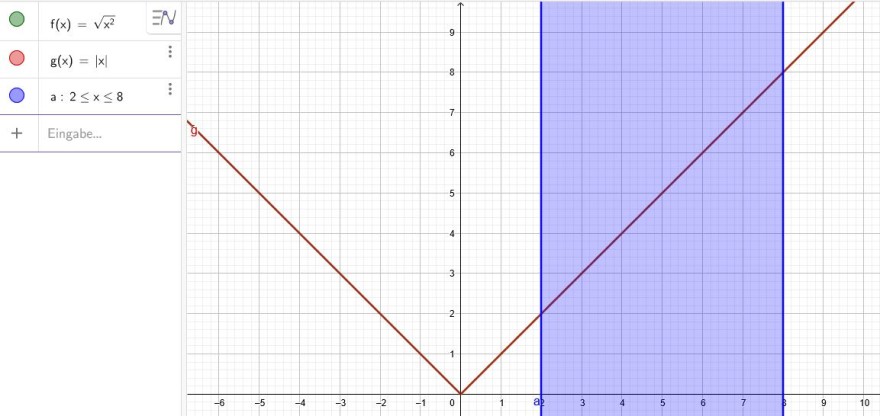
\(f(x)= \sqrt{x^2}=|x| \) mit \(2≤x≤8\)
\(r_1=f(2)= \sqrt{2^2}=|2|=2 \)
\(r_2=f(8)= \sqrt{8^2}=|8|=8 \)
Dies gilt bei der Rotation um die x-Achse.
Da \(f(x)=|x|\) ist gilt \(y=x\) im Intervall \([0≤x≤∞)\) und \(y=-x\) im Intervall \((-∞≤x≤0]\)
Somit ist auch der Radius bei der Rotation um die y-Achse analog zum Radius \(r_1und r_2 \)