Aufgabe:
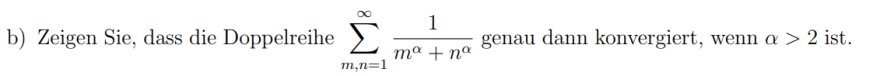
Text erkannt:
b) Zeigen Sie, dass die Doppelreihe \( \sum \limits_{m, n=1}^{\infty} \frac{1}{m^{\alpha}+n^{\alpha}} \) genau dann konvergiert, wenn \( \alpha>2 \) ist.
Problem/Ansatz:
Meine Problem ist hier wie man hier vorgehen soll. Auf Konvergenz zu untersuchen ist kein Problem, nur steht da Doppelreihe. Muss ich die Doppelreihe sozusagen "auseinanderziehen" und dann erst auf Konvergenz überprüfen und was genau muss ich bei dem α>2 beachten ?
Ein Ansatz wäre super !
Vielen Dank !