Konvergenz der Fourierreihe-Verständnisfrage

Question

Aufgabe:

Ich habe eine Fourierreihe bestimmt und das Ergebnis lautet:

Φ(x)=\( \sum\limits_{n=1}^{\infty}{n} \)b_n(nπx) mit b_n=-\( \frac{4}{nπ} \) für ungerade n und b_n=0 für gerade n.

Der Vollständigkeit halber hier noch die gegebene Funktion:

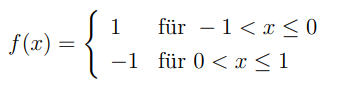
Text erkannt:

\( f(x)=\left\{\begin{array}{ll}1 & \text { für }-1<x \leq 0 \\ -1 & \text { für } 0<x \leq 1\end{array}\right. \)

Nun sollen wir im Aufgabenteil b.) bestimmen, für welche x die Reihe gegen f(x) konvergiert.

Da ich überhaupt keine Idee hatte, wie ich an diese Sache heran gehe, habe ich in der Musterlösung nachgeschaut und dort stand: x∈ℝ\ℤ.

Jetzt frage ich mich warum das so ist.

Vielen Dank im Voraus :)

Answer 1

Das ist einfach die Aussage eines Satzes. Die Funktion f ist auf Teilintervallen stetig und monoton. An den Unstetigkeitsstellen liegen nur Sprungstellen vor (also z.B. keine Pole....). Dann konvergiert die Fourier-Reihe an allen Stetigkeitsstellen gegen f(x), an den Sprungstellen gegen das arithmetische Mittel der beiden einseitigen Grenzwerte.

Dieser Satz wird oft als Dirichlet-Bedingungen zitiert. Der Beweis ist nicht trivial (für meinen Horizont); deshalb bin ich mir sicher, dass Du diesen oder einen ähnlichen Satz in Deine Lehrmaterial findest.