Hey, seht ihr vielleicht, wie man auf diese Varianz beziehungsweise diesen Erwartungswert kommt? Ich verstehe nicht so ganz, wieso der erste Teil (1-2/sqrt(n)) zur Berechnung der Varianz bzw. des Erwartungswert weggelassen worden ist. Oder sehe ich das falsch?

Text erkannt:
Aufgabe \( 3(5 \mathrm{P}) \). Sei \( X_{n, i}:(\Omega, \mathcal{A}, P) \rightarrow \mathbb{R} \) ein Dreiecksschema von zeilenweise unabhängigen Zufallsvariablen, \( 1 \leq i \leq n \) und \( 3 \leq n \in \mathbb{N} \), mit
\( P_{X_{n, i}}=\left(1-\frac{2}{\sqrt{n}}\right) \varepsilon_{0}+\frac{1}{\sqrt{n}} \varepsilon_{n}+\frac{1}{\sqrt{n}} \varepsilon_{-n} . \)
Sei \( T_{n}:=\sum \limits_{i=1}^{n} X_{n, i} \).
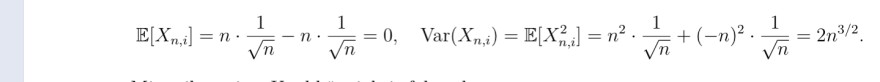
Text erkannt:
\( \mathbb{E}\left[X_{n, i}\right]=n \cdot \frac{1}{\sqrt{n}}-n \cdot \frac{1}{\sqrt{n}}=0, \quad \operatorname{Var}\left(X_{n, i}\right)=\mathbb{E}\left[X_{n, i}^{2}\right]=n^{2} \cdot \frac{1}{\sqrt{n}}+(-n)^{2} \cdot \frac{1}{\sqrt{n}}=2 n^{3 / 2} \)
Ich wäre super danke für eure Hilfe.
LG