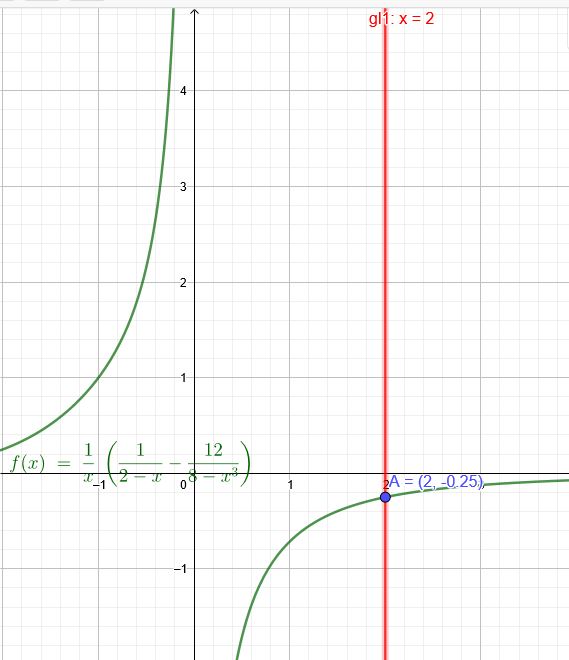
\( \lim \limits_{x \rightarrow 2} \frac{1}{x}*\left(\frac{1}{2-x}-\frac{12}{8-x^{3}}\right) \)
\( \frac{1}{x}*(\frac{1}{2-x}-\frac{12}{8-x^3}) \)=
Einschub: \(8-x^3=(2-x)*(x^2+2x+4)\)
=\( \frac{1}{x}*(\frac{1}{2-x}-\frac{12}{(2-x)*(x^2+2x+4)}) \)=
=\( \frac{1}{x}*(\frac{x^2+2x+4}{(2-x)*(x^2+2x+4)}-\frac{12}{(2-x)*(x^2+2x+4)}) \)=
=\( \frac{1}{x}*(\frac{x^2+2x-8}{(2-x)*(x^2+2x+4)})\)=
=\( \frac{1}{x}*(\frac{(x+4)*(x-2)}{(2-x)*(x^2+2x+4)})\)=
=\( \frac{1}{x}*(-\frac{(x+4)*(2-x)}{(2-x)*(x^2+2x+4)})\)=
=\( \frac{1}{x}*(-\frac{(x+4)}{(x^2+2x+4)})\)=
=\( (-\frac{(x+4)}{(x^3+2x^2+4x)})\)=
\(x=2\)
\( (-\frac{(2+4)}{(2^3+2*2^2+4*2)})\)= \( (-\frac{(6)}{(8+8+8)})\)=\( (-\frac{(6)}{24)})\)=
\( (-\frac{1}{4)})\)
\( \lim \limits_{x \rightarrow 2} \frac{1}{x}*\left(\frac{1}{2-x}-\frac{12}{8-x^{3}}\right)=-\frac{1}{4} \)