Hallo,
Wenn man einen Punkt \(P\) an einer Geraden spiegelt, so wäre eine Lösung, die Projektion (den Fußpunkt \(F\)) auf eben der Geraden zu berechnen und anschließend den Punkt \(P\) an \(F\) zu spiegeln.
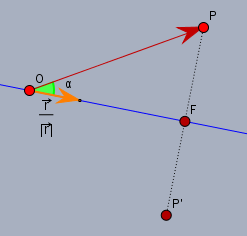
Das Spiegelbild von \(P\) ist dann \(P'\)$$P' = F + (F-P) = 2F - P$$und für den Fußpunkt \(F\) gilt$$F = \frac{\vec{r}}{|\vec{r}|} \underbrace{\left<\frac{\vec{r}}{|\vec{r}|},\, P\right>}_{\cos(\alpha) \cdot |P| = |OF|}$$der orange farbende Vektor ist der Einheitsvektor \(\vec{r}/|\vec{r}|\) in Richtung der Geraden. Hier ist:$$\vec{r}= \begin{pmatrix} -1\\0\\1 \end{pmatrix}$$Der Term in spitzen Klammern ist das Skalarprodukt des Einheitsvektors mit dem Ortsvektor von \(P\) und damit gleichzeitig der (vorzeichenbehaftete) Abstand |OF|.
Das ganze in Matrixschreibweise gibt dann$$\begin{aligned} F &= \frac{\vec{r}}{|\vec{r}|} \left<\frac{\vec{r}}{|\vec{r}|},\, P\right> \\ &= \frac{1}{|\vec{r}|^2} \vec{r}\vec{r}^T P \end{aligned}$$Beachte, das es sich bei \(\vec{r}\vec{r}^T\) um das dyadische Produkt handelt, also um eine Matrix. Und zum Spiegelpunkt \(P'\) kommt man dann über$$P' = 2F - P = \frac{2}{|\vec{r}|^2} \vec{r}\vec{r}^T P - P \\ \phantom{P'} = \left( \frac{2}{|\vec{r}|^2} \vec{r}\vec{r}^T - \underline 1\right)P$$und der Term vor dem \(P\) ist bereits die gesuchte Matrix. Man braucht nur noch das \(\vec{r}\) einzusetzen:$$\frac{2}{|\vec{r}|^2} \vec{r}\vec{r}^T - \underline 1 = \frac{2}{2}\begin{pmatrix}1& 0& -1\\ 0& 0& 0\\ -1& 0& 1\end{pmatrix} - \begin{pmatrix}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{pmatrix} \\ \phantom{\frac{2}{|\vec{r}|^2} \vec{r}\vec{r}^T - \underline 1}= \begin{pmatrix}0& 0& -1\\ 0& -1& 0\\ -1& 0& 0\end{pmatrix}$$
Der Weg, den Dir abakus vorgeschlagen hat, geht über die räumliche Vorstellung. Sieh Dir dazu folgende Szene in Geoknecht3D an:
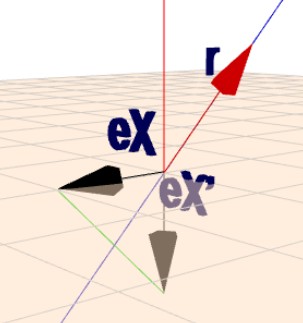
Klick auf das Bild und rotiere die Szene mit der Maus, damit Du eine bessere räumliche Vorstellung bekommst.
Die gegebene Ursprungsgerade ist blau eingezeichnet. Den Einheitsrichtung in X-Richung \(e_x=(1|0|0)\) habe ich schwarz eingezeichnet. Da die Spiegelgerade gleichzeitig die Winkelhalbierende von \(X\) und \(-Z\) ist, ist offensichtlich das Spiegelbild von \(e_{x}\)$$e_{x}' = \begin{pmatrix}0\\ 0\\ -1\end{pmatrix}$$und so einfach kommst Du auch zu \(e_{y}'\) und \(e_{z}'\). Stelle die drei gespiegelten Vektoren neben einander und Du erhältst die gewünschte Matrix.
Gruß Werner