Wenn ich die Lösung allerdings nicht kennen würde, wie würde ich dann vorgehen?

Question

Aufgabe: Beweise das folgende Aussage über Mengen wahr ist oder gib ein Gegenbeispiel an.

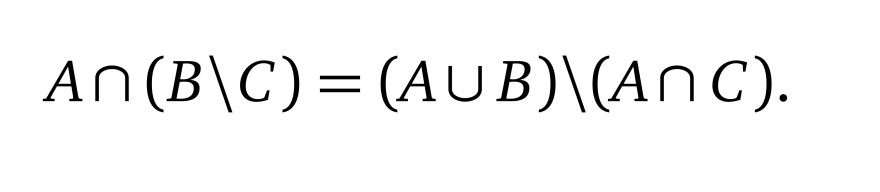
Text erkannt:

\( A \cap(B \backslash C)=(A \cup B) \backslash(A \cap C) \)

Problem/Ansatz:

Ich habe die Lösung zu der Aufgabe. Die Aussage ist falsch und ich habe auch ein Gegenbeispiel. Wenn ich die Lösung allerdings nicht kennen würde, wie würde ich dann vorgehen? Ich müsste ja zuerst beweisen, dass die Aussage falsch ist, oder?

Mein Ansatz ist folgender: um Gleichheit zu beweisen muss überprüft werden, ob die linke Menge Teilmenge der Rechten ist und umgekehrt. Dafür kann ich im ersten Fall sagen, dass x in A, B aber nicht in C sein kann. Ist das soweit ein richtiges Vorgehen? Weiter komme ich leider nicht

Answer 1

Ich fand es früher immer sehr hilfreich, die Mengen im Venn-Diagramm zu skizzieren.

Günstig ist es auch, die Terme jeweils zu vereinfachen. Dann ist auch klar, dass es nicht dasselbe ist.

Comments

Ich denke, dass die (reichliche) Verwendung von Klammern, wie sie der Fragesteller auch gesetzt hat, bei solchen Aufgaben sehr nützlich (oder gar notwendig !) ist.

---

Danke für die Hilfe! Auf welcher Seite wurden diese Diagramme erstellt?

---

Ich denke, dass die (reichliche) Verwendung von Klammern, wie sie der Fragesteller auch gesetzt hat, bei solchen Aufgaben sehr nützlich (oder gar notwendig !) ist.

Wolframalpha hat die Klammern weggelassen, obwohl ich sie eingegeben habe. Wenn man sich das Venn-Diagramm ansieht, hat er es doch aber richtig interpretiert.

Danke für die Hilfe! Auf welcher Seite wurden diese Diagramme erstellt?

Wolframalpha, der Taschenrechner für Studenten.

https://www.wolframalpha.com