Bestimmen Sie Polynome q, r ∈ ℤ_{3}[x] , so dass gilt:

Question

Aufgabe:

Hey, Leute, ich habe ein Problem bei einer Mathematik- Aufgabe aus dem Modul Lineare Algebra 1. Ich bräuchte bitte Hilfe.

Problem/Ansatz:

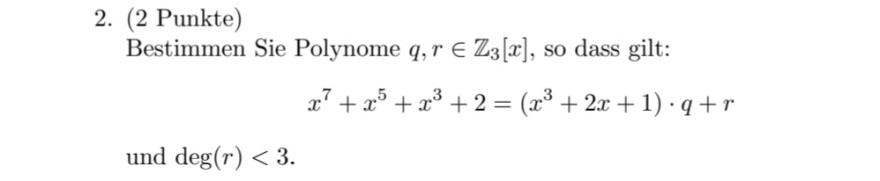
Text erkannt:

2. (2 Punkte)
Bestimmen Sie Polynome \( q, r \in \mathbb{Z}_{3}[x] \), so dass gilt:
\( x^{7}+x^{5}+x^{3}+2=\left(x^{3}+2 x+1\right) \cdot q+r \)
und \( \operatorname{deg}(r)<3 \).

Was muss ich hier an der Stelle beachten, wenn ich statts in R[x] hier in Z3[x] rechne? Ich weiß, dass das ein Restklassenring ist. Aber ich bekomme die Division einfach nicht hin. Wäre nett, wenn ihr mir helfen könntet. Vielen lieben Dank im voraus.

Answer 1

Es gilt x^5 ≡ x mod 3.

Damit kannst du x^5 durch x und x^7 durch x^3 ersetzen. Das vereinfacht das gegebene Polynom.

Comments

Ok. Also ich ersetze nur die Polynome, aber der restliche Ablauf bezüglich des Rechnens ist genauso wie bei der Menge R[x]?

---

Richtig, durch die Ersetzung von x⁵ durch x und x⁷ durch x³ vereinfachst du das gegebene Polynom. Der restliche Ablauf der Division, also die Berechnung von q und r, erfolgt genauso wie in der Menge R[x]. Der Unterschied besteht darin, dass die Division in Z3[x] modulo 3 durchgeführt wird, das heißt die Ergebnisse der Division müssen in Z3[x] liegen. Dazu musst du beim Rechnen also sicherstellen, dass jedes Ergebnis modulo 3 reduziert wird.

---

Ich habe es jetzt mal selbst probiert. Kann jemand vielleicht einen Fehler erkennen?

Text erkannt:

\( \left(x^{7}+x^{5}+x^{3}+2\right):\left(x^{3}+2 x+1\right)=\underbrace{x^{4}+2 x^{2}}_{7} \)
\( \frac{-\left(x^{7}+2 x^{5}+x^{4}\right)}{0-x^{5}-x^{4}} \quad d a-1 \equiv 2(\bmod (3) \)
\( 2 x^{5}+2 x^{4} \Leftrightarrow 1 \)
\( \frac{-\left(2 x^{5}+4 x^{3}+2 x^{2}\right)}{0-4 x^{3}-2 x^{2}+x^{3}} \)
\( -3 x^{3}-2 x^{2} \)
\( \frac{x^{2}+2}{r} \quad \Leftrightarrow \quad-3 \equiv 0(\operatorname{mos}(3) \)
\( -2=1 \)

---

Wenn man die beiden Ersetzungen vornimmt, vereinfacht sich der Term zu 2x³+x+2.

Da x kongruent zu 4x mod 3 ist, kann man das ersetzen und erhält 2x³+4x+2..

Wenn man das durch den Term x³+2x+1 teilt, erhält man q=2 und den Rest r=0.

---

Das \(x\) in \(K[x]:=\mathbb{Z}_3[x]\) ist eine Unbestimmte.
\(x^5=x\) in \(K[x]\) würde bedeuten, dass \(x\)
algebraisch über \(K\) wäre.

---

Man kann also \(x^5\) nicht durch \(x\) ersetzen;
denn in dieser Aufgabe ist die Rede von Polynomen
und nicht von polynomialen Abbildungen.

---

Vielen lieben Dank, ermanus,

das habe ich mir nämlich auch schon gedacht, dass eine Ersetzung der Polynome hier nicht möglich ist. Danke für deinen Kommentar.