fang an mit einer planfigur!
die aufgabe läßt sich in zwei drehungen um die koordinaten achsen zerlegen.
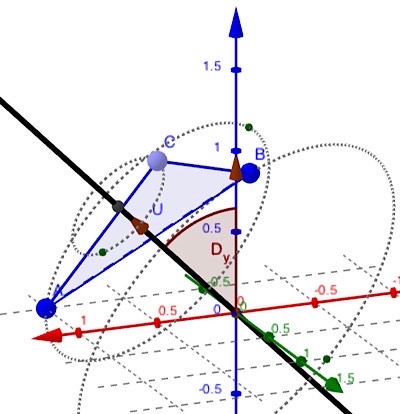
die drehachse liegt in der xz-ebene in einem winkel (x=1,0,z=1)=45 grad.
du drehst über die y-achse um -45 grad matrix Dy in die z-achse über die die eigentliche drehung von 90 grad Matrix Dz und machst dann Dy rückwärts (rückgängig).
eine gesamtbetrachtung zu elementaren achsendrehungen findest du unter
https://www.geogebra.org/m/NXx4E8cb