Beweis dass sich Umkreise treffen?

Question

Aufgabe:

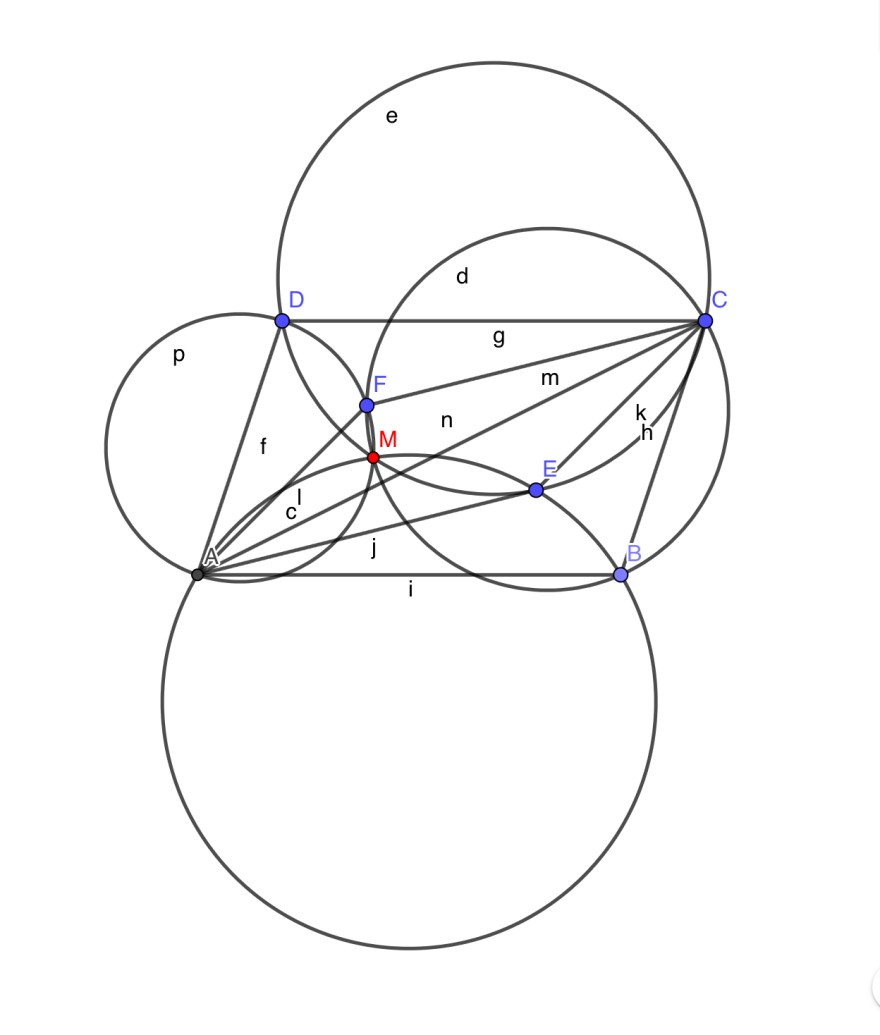
Es gibt zwei Parallelogramme ABCD und AECF mit gemeinsamer Diagonale AC, wobei E und F im Inneren des Parallelogramms ABCD liegen.
Beweisen Sie, dass die Umkreise der Dreiecke AEB, BFC, CED und DFA einen Punkt gemeinsam haben.

Problem/Ansatz:

Mein Ansatz ist es, zu beweisen, dass AMFD zyklisch ist, so dass sich die Umkreise an dem gemeinsamen Punkt treffen, den ich M genannt habe. AMFD reicht aufgrund verschiedener Symmetrien in der Figure aus, was bedeuten würde, dass der Beweis der zyklischen AMFD gleichbedeutend wäre mit beweisen, dass MBFC zyklisch ist. Ich möchte dies mit Angle Chasing tun, aber irgendwie bekomme ich nichts heraus. Könnte mir jemand helfen?

Comments

Die Aufgabensteller beim BWM werden sich über den Daumen freuen.

---

Danke hj2166!

https://www.google.com/url?sa=t&source=web&rct=j&url=https://www.mathe-wettbewerbe.de/fileadmin/Mathe-Wettbewerbe/Bundeswettbewerb_Mathematik/Dokumente/BWM_2023.1_Aufgabenblatt.pdf&ved=2ahUKEwiWoY6zgvL8AhUvQ_EDHZQPC1MQFnoECB4QAQ&usg=AOvVaw0kZP5MySC7R8mopnw82IM6

@Erik:

Selbstständigkeitsverpflichtung: Mit Deiner Teilnahme verpflichtest Du Dich bzw. verpflichtet Deine Gruppe sich zur selbstständigen Arbeit gemäß der Selbstständigkeitserklärung, die Du auf dem Teilnahmecoupon unterschreiben musst. Die Verpflichtung zur Selbstständigkeit gilt schon für die Phase der Lösungsfindung und nicht erst für die endgültige Formulierung. Diskussionen von Lösungswegen, insbesondere im Internet, sind nicht zulässig. Ein begründeter Verdacht auf Verstoß gegen die Selbstständigkeitsverpflichtung führt zum Ausschluss vom Wettbewerb.