Aufgabe: gerade oder ungerade Funktion (zur Bestimmung der Fourrierkoeffizienten)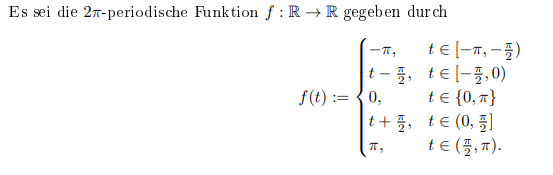
Text erkannt:
Es sei die \( 2 \pi \)-periodische Funk tion \( f: \mathbb{R} \rightarrow \mathbb{R} \) gegeben durch
\( f(t):=\left\{\begin{array}{ll} -\pi, & t \in\left[-\pi,-\frac{\pi}{2}\right) \\ t-\frac{\pi}{2}, & t \in\left[-\frac{\pi}{2}, 0\right) \\ 0, & t \in\{0, \pi\} \\ t+\frac{\pi}{2}, & t \in\left(0, \frac{\pi}{2}\right] \\ \pi, & t \in\left(\frac{\pi}{2}, \pi\right) . \end{array}\right. \)
…
Problem/Ansatz: Mir ist nicht ganz klar,warum es sich bei dieser Fuktion um eine ungerade Funktion handelt,denn
es gilt ja beispielsweise,dass f(-π) = -π, aber -f(π)= 0,was ja ein Widerspruch zur Definition von ungeraden Funktionen wäre.