Hallo zusammen, ich soll die folgende Aufgabe mittels des Majoranten-/ Minorantenkriterium auf Konvergenz überprüfen.
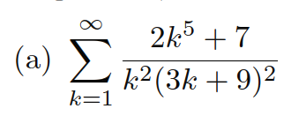
Text erkannt:
(a) \( \sum \limits_{k=1}^{\infty} \frac{2 k^{5}+7}{k^{2}(3 k+9)^{2}} \)
Problem/Ansatz:
Ich habe den unteren Term mal ausmultipliziert und kam dafür auf 19k4+ 81k²+54k³, mein Problem ist jedoch, das der Zähler mit 2k5 ja einen höheren Exponenten hat, das hatte ich so in einer Aufgabe noch nie. Um die Aufgabe zu lösen muss ich ja immer auf (1/k)x kommen, oder? Hierfür fehlt mir nämlich leider der Ansatz.
Ich bin für jede Hilfe dankbar!