Äußere und innere Tangente (Abstand)

Question

Aufgabe:

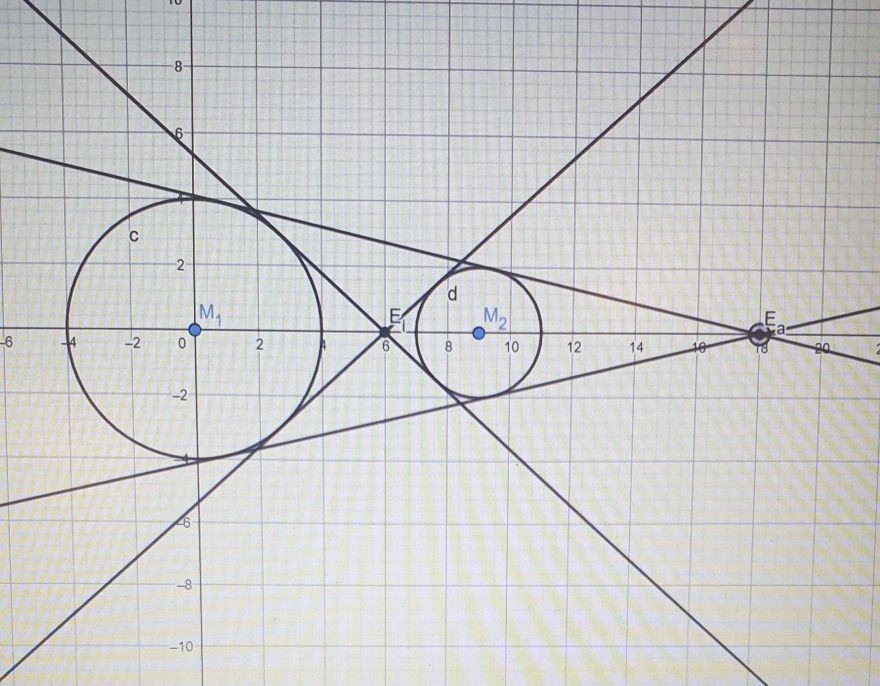
Gegeben seien 2 Kreise $k_{1}$ und $k_{2}$ mit Mittelpunkten $M_{1}$ und $M_{2}$ und Radien $r_{1}=4 \mathrm{~cm}$ und $r_{2}=2 \mathrm{~cm}$. Der Abstand der Mittelpunkte betrage $9 \mathrm{~cm} . E_{i}$ sei der Schnittpunkt der gemeinsamen inneren Tangenten beider Kreise, $E_{a}$ sei der Schnittpunkt der gemeinsamen äußeren Tangenten beider Kreise.

Machen Sie eine Skizze. Berechnen Sie die Abstände $d_{i}=\left|M_{1} E_{i}\right|$ und $d_{a}=\left|M_{1} E_{a}\right|$. Begründen Sie ihren Rechenweg.

Ich habe dazu eine Skizze gemacht und nach geogebra komme ich auf |M1Ei|= 6 und |M2Ea|= 9.

Ich habe versucht mir eine grobe Rechnung zu definieren, z.B. dass Ei immer r1 + r2 ist und Ea = 2×|M1M2|. Für andere Kreise mit unterschiedlichen Abständen geht die Rechnung aber nicht auf. Würde mich über Hilfe sehr freuen. Ich verstehe nämlich nicht, wie ich ohne geogebra darauf komme :D (für x beliebige Kreise mit x beliebigen Radien und Abständen etc.)

Comments

wie ich ohne geogebra darauf komme

Mit Geogebra kommst Du auch nicht darauf. Nur Geogebra kommt darauf.

Ohne Geogebra kannst Du mit den Strahlensätzen darauf kommen.

---

Geogebra dient nur als Ersatz zu Zirkel, Lineal und Bleistift. Ich traue dem Anwender also auch zu, das er selber eine zeichnerische Lösung finden würde, auch ohne Geogebra.

Geogebra allein ist strohdumm und kann solche Aufgaben ohne einen Anwender auch nicht allein lösen.

Answer 1

Strahlensatz

sei x = M2Ea

x/2 = (x + 9)/4 → x = 9 cm

sei y = M2Ei

y/2 = (9 - y)/4 --> y = 3 cm

Comments

Alles klar, danke dir vielmals!!! Das hilft mir ordentlich weiter :))

Answer 2

Ich habe mal 2 Zeichnungen für die Konstruktion der inneren und der äußeren Tangenten zweier Kreise eingestellt. Vielleicht ist das eine Hilfe:

Comments

Ich danke dir für deine Mühen!