Aloha :)
Willkommen in der Mathelounge... \o/
Wir suchen zunächst die Extrempunkte der Funktion$$f(x;y)=3x^2+4y^2-x+3$$ohne die Nebenbedingung zu beachten.
Kandidaten für Extremwerte finden wir an den Nullstellen des Gradienten:$$\binom{0}{0}\stackrel!=\operatorname{grad}f(x;y)=\binom{6x-1}{8y}\implies\binom{x}{y}=\binom{\frac16}{0}$$
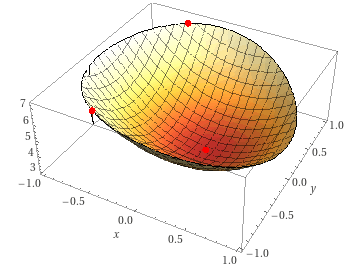
Wir prüfen den Kandidaten mittels der Hesse-Matrix:$$H(x;y)=\left(\begin{array}{rr}6 & 0\\0 & 8\end{array}\right)$$Die Eigenwerte \(6\) und \(8\) der Hesse-Matrix sind positiv, also ist die Hesse-Matrix positiv definit, sodass ein lokales Minimum vorliegt.$$\text{Min}\left(\frac16\bigg|0\right)\quad;\quad f\left(\frac16;0\right)=\frac{35}{12}$$
Das gefundene Minimum erfüllt insbesondere die Nebenbedingung, denn:$$2\cdot\left(\frac16\right)^2+2\cdot0^2=\frac{1}{18}\le2\quad\checkmark$$
Am Rand der Nebenbedingung, also für \((2x^2+2y^2\pink=2)\) könnten sich noch Randextrema befinden. Wir schreiben daher die Funktion \(f(x;y)\) unter der Randbedingung um und bestimmen ihre möglichen Extremwerte:$$f(x;y)=3x^2+4y^2-x+3=3x^2+(4-4x^2)-x+3=-x^2-x+7\eqqcolon g(x)$$Die Funktion \(g(x)\) besitzt lokale Maxima, denn:$$g'(x)\stackrel!=0\implies-2x-1=0\implies x=-\frac12\quad;\quad g''(x)=-2<0\quad\text{(Maximum)}$$
Setzen wir \((x=-\frac12)\) in die Nebenbedingung ein, erhalten wir \((y=\pm\frac12\sqrt3)\) und können somit zwei Randmaxima angeben:$$\text{Max}\left(-\frac12\bigg|\pm\frac{\sqrt3}{2}\right)\quad;\quad f\left(-\frac12\bigg|\pm\frac{\sqrt3}{2}\right)=\frac{29}{4}$$
Alle 3 Extremwerte sind global, das Minimum beschreibt das einzige und damit globale Minimum der Funktion. Die beiden Maxima liegen auf dem äußersten Rand der Nebenbedingung und sind beide gleich groß.