Extrema mit Nebenbedingung

Question

Aufgabe

f(x,y) = 3x²+4y² -x + 3. globale extrempunkte ermitteln unter NBd. 2x² +2y² <= 2

Problem/Ansatz

ich komme irgrndwie nicht auf die richtige Lösung. Hab die Nebenbedingung nach y² umgestellt und in die die Funktion eingesetzt aber erhalte trotzdem ein falsches Ergebnis

ich hoffe ihr könnt mir helfen. kann man dies lösen ohne Anwendung von Lagrange

Comments

Hab die Nebenbedingung nach y^2 umgestellt und in die die Funktion eingesetzt

Nicht behaupten. Zeigen!  

---

y²<= 1-x²

f(x) = 3x² +4*(1-x²)²+3

f(x)=4x⁴ - 5x² - x +7

f'(x) = 16x³ - 10x -1

x1,x2,x3 = 0,74 , 0,83, -0,1

aber das sind nunmal die falschen x-werte

*EDIT: pardon ich bin wirklich ein dussel, hab das y quadriert und eben erst beim eintippen gesehen. Ich saß ungelogen 1-2 Stunden an der Aufgabe und hab immer wieder neugerechnet

---

Wenn du y² durch 1-x² ersetzen willst, dann tu das einfach. Aber warum willst du dieses (1-x²) nochmal quadrieren?

Denke außerdem daran, dass y²<= 1-x² keine Gleichung, sondern eine Ungleichung ist.

Answer 1

Aloha :)

Willkommen in der Mathelounge... \o/

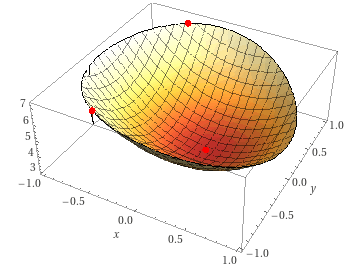
Wir suchen zunächst die Extrempunkte der Funktion$$f(x;y)=3x^2+4y^2-x+3$$ohne die Nebenbedingung zu beachten.

Kandidaten für Extremwerte finden wir an den Nullstellen des Gradienten:$$\binom{0}{0}\stackrel!=\operatorname{grad}f(x;y)=\binom{6x-1}{8y}\implies\binom{x}{y}=\binom{\frac16}{0}$$

Wir prüfen den Kandidaten mittels der Hesse-Matrix:$$H(x;y)=\left(\begin{array}{rr}6 & 0\\0 & 8\end{array}\right)$$Die Eigenwerte $6$ und $8$ der Hesse-Matrix sind positiv, also ist die Hesse-Matrix positiv definit, sodass ein lokales Minimum vorliegt.$$\text{Min}\left(\frac16\bigg|0\right)\quad;\quad f\left(\frac16;0\right)=\frac{35}{12}$$

Das gefundene Minimum erfüllt insbesondere die Nebenbedingung, denn:$$2\cdot\left(\frac16\right)^2+2\cdot0^2=\frac{1}{18}\le2\quad\checkmark$$

Am Rand der Nebenbedingung, also für $(2x^2+2y^2\pink=2)$ könnten sich noch Randextrema befinden. Wir schreiben daher die Funktion $f(x;y)$ unter der Randbedingung um und bestimmen ihre möglichen Extremwerte:$$f(x;y)=3x^2+4y^2-x+3=3x^2+(4-4x^2)-x+3=-x^2-x+7\eqqcolon g(x)$$Die Funktion $g(x)$ besitzt lokale Maxima, denn:$$g'(x)\stackrel!=0\implies-2x-1=0\implies x=-\frac12\quad;\quad g''(x)=-2<0\quad\text{(Maximum)}$$

Setzen wir $(x=-\frac12)$ in die Nebenbedingung ein, erhalten wir $(y=\pm\frac12\sqrt3)$ und können somit zwei Randmaxima angeben:$$\text{Max}\left(-\frac12\bigg|\pm\frac{\sqrt3}{2}\right)\quad;\quad f\left(-\frac12\bigg|\pm\frac{\sqrt3}{2}\right)=\frac{29}{4}$$

Alle 3 Extremwerte sind global, das Minimum beschreibt das einzige und damit globale Minimum der Funktion. Die beiden Maxima liegen auf dem äußersten Rand der Nebenbedingung und sind beide gleich groß.