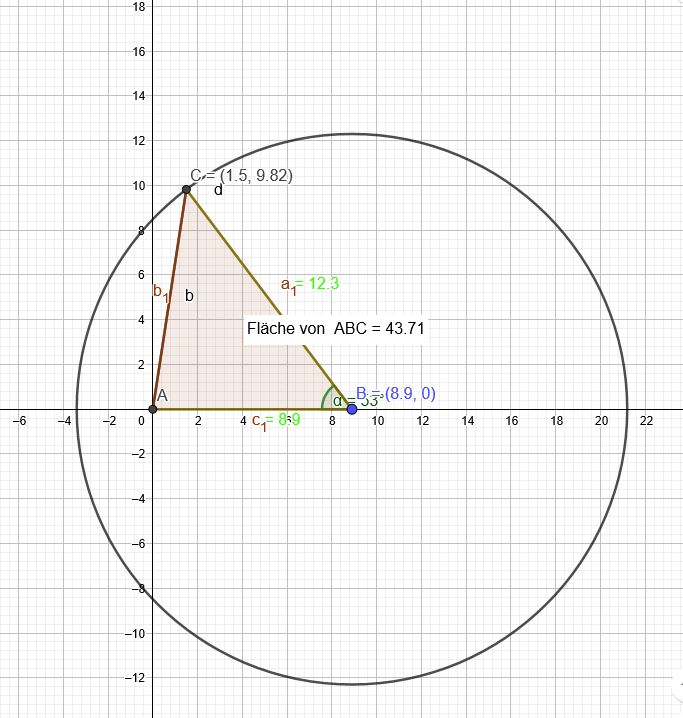
1) Berechne den Flächeninhalt des Dreiecks ABC mit
\(a = 12,3 cm; c = 8,9 cm; β = 53°\)
Berechnung der Geraden durch \(B(8,9|0)\) mit \(β = 53°\):
\(tan(-53°)≈-1,327\)
\( \frac{y-0}{x-8,9}=-1,327 \) → \( y=-1,327*(x-8,9) \) → \( y=-1,327*x+11,8103 \)
Berechnung der Koordinaten von C:
Kreis um \(B(8,9|0)\) mit \(a=r=12,3\)
\((x-8,9)^2+y^2=12,3^2\) → \((x-8,9)^2+(-1,327*x+11,8103)^2=12,3^2\)
\(x≈1,5\) \( h=y=-1,327*1,5+11,8103≈9,82 \)
\(A= \frac{1}{2}*c*h \) \(A= \frac{1}{2}*8,9cm*9,82cm≈43,7cm^{2} \)