Aufgabe:
Familie Sonnberg will einen neuen Schirmständer für ihre Veranda kaufen. Vater Bernd ist begeistert und holt auch schon seine Zeichnung hervor, um der Familie zu zeigen, dass man den auch selbst anfertigen kann. Alle schauen gespannt seinen Ausführungen zu, bis Marie sagt: \( { }_{n} \) Wenn der wirklich aus Eisen ist, kann den niemand tragen!" Was meinst du, stimmt das? Schätze erst und berechne anschließend die Masse für eine Dichte von \( 7,86 \frac{\mathrm{g}}{\mathrm{cm}^{3}} \) (Eisen).
Musterlösung:
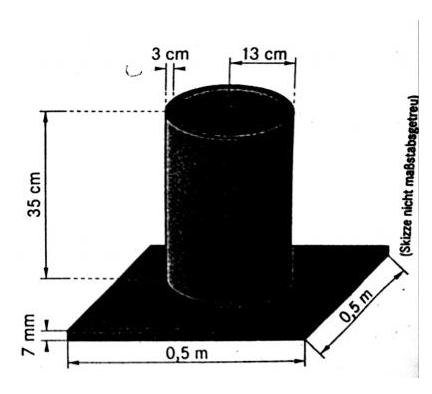
Der Schirmständer besteht aus (I) Hohlzylinder mit \( r_{a}=13 \mathrm{~cm}, r_{i}=10 \mathrm{~cm}, h=35 \mathrm{~cm} ; \) (II) Quader mit \( a=b=50 \mathrm{~cm}, h=0,7 \mathrm{~cm} \)
Volumen: (I) \( V_{1}=7586,95 \mathrm{~cm}^{3} \); (II) \( V_{2}=1750 \mathrm{~cm}^{3} \); gesamtes Volumen: \( V_{\text {ges }}=9336,95 \mathrm{~cm}^{3} \) Masse = Dichte \( \cdot \) Volumen: Masse des Schirmständers: \( m=73,4 \mathrm{~kg} \) Der Schirmständer ist mit über \( 70 \mathrm{~kg} \) für den alltäglichen Gebrauch wirklich zu schwer.