Berechne eine mögliche Funktionsgleichung der zugehörigen Parabel

Question

                                                                Das Spielfeld ist 18 m lang

Aufgabe 1: Berechne eine mögliche Funktionsgleichung der zugehörigen Parabel.

Aufgabe 2: Berechne, in welchem Abstand  der Ball das Netz überquert.

Aufgabe 3: Bestimme wie weit von der Auslinie entfernt kommt der Ball auf den Boden aufkommt.

Problem/Ansatz:  Der Ball wird von unten in einer höhe von 90 cm über den Boden abgeschlagen und der Ball erreicht nach 8,1 m (horizontal gemessen) die maximale Höhe von 3,9 m. Wie kann ich mit diesen Zahlen Aufgabe 1 Berechnen.

Wie Berechne ich Aufgabe 2 (Abstand Ball zum Netz) Wenn mir die Zahl 2,24 m gegeben ist?

Answer 1

Hallo,

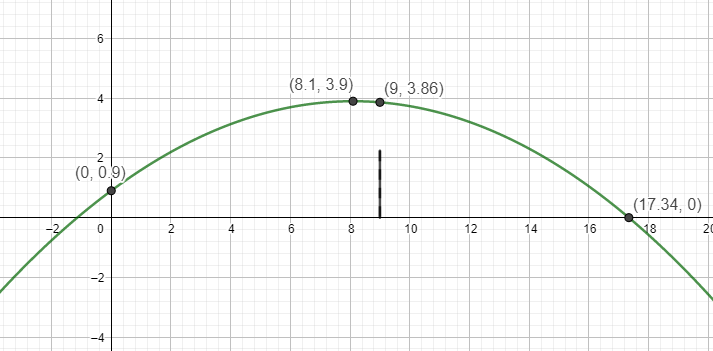
Scheitelpunktform einer quadratischen Funktion \(f(x)=a(x-d)^2+e\) mit dem Scheitelpunkt S (d | e), hier (8,1 | 3,9)

\(f(x)=a(x-8,1)^2+3,9\)

Um a zu bestimmen, setzt du die Koordinaten des Punktes (0 | 0,9) in die Gleichung ein

\(0,9=a(0-8,1)^2+3,9\) und löst nach a = -0,457 auf.

Damit lautet eine mögliche Funktionsgleichung der Parabel

\(f(x) =-0,0457(x-8,1)^2+3,9\)

Berechne, in welchem Abstand der Ball das Netz überquert.

Das Netzt befindet sich in der Mitte des Platzes bei x = 9. Berechne f(9) und dann die Differenz zu 2,24.

Bestimme wie weit von der Auslinie entfernt kommt der Ball auf den Boden aufkommt.

Berechne die Nullstellen der Funktion und dann die Differenz zwischen der positiven Nullstelle und 18.

Gruß, Silvia

Answer 2

Der Ball wird von unten in einer höhe von 90 cm über den Boden abgeschlagen und der Ball erreicht nach 8,1 m (horizontal gemessen) die maximale Höhe von 3,9 m.

Benutze http://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm zur Hilfe und Selbstkontrolle

Eigenschaften

f(0) = 0.9
f(8.1) = 3.9
f'(8.1) = 0

Gleichungssystem

c = 9/10
6561/100·a + 81/10·b + c = 39/10
81/5·a + b = 0

Funktion

f(x) = -100/2187·x² + 20/27·x + 9/10

Aufgrund der Netzhöhe gehe ich mal von einem Volleyballfeld aus. Der Abschlag wird dann vermutlich von der Grundlinie durchgeführt. Aber solche Angaben sollten eigentlich auch alle in der Aufgabe stehen und sollten sich nicht vom Bearbeiter der Aufgabe ausgedacht werden.