Hallo,
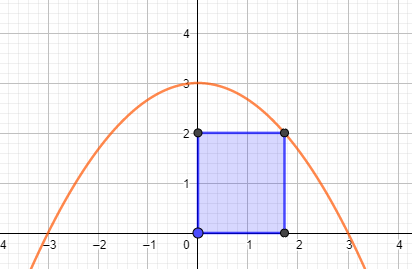
die Nullstellen sind bei -3 und 3 und der Scheitelpunkt hat die Koordinaten S (0|3).
Also ist \(f(x)=a(x-3)(x+3)\). Um a zu bestimmen, setze die Koordinaten von S ein.
Damit ist \(f(x)=-\frac{1}{3}(x-3)(x+3)\\ =-\frac{1}{3}x^2+3\)
Flächeninhalt eines Rechtecks ist \(A=a\cdot b\).
a = x und b = f(x)
Damit lautet die Gleichung für den Flächeninhalt
\(A=x\cdot(-\frac{1}{3}x^2+3)=-\frac{1}{3}x^3+3x\)
Bilde davon die 1. Ableitung, setze sie = 0 und löse nach x auf.
\(A'=-x^2+3\\ -x^2+3=0\\ x^2=3\\x=\sqrt{3}\)
\(x=- \sqrt{3} \) fällt weg, das sich das Rechteck im 1. Quadranten befinden soll.
Gruß, Silvia