Hallo,
du hast dich leider verrechnet.
satt \(x\cdot (x+6)=0\) muss es heißen \(x\cdot (2x+6)=0\). Daraus folgt dann x = -3.
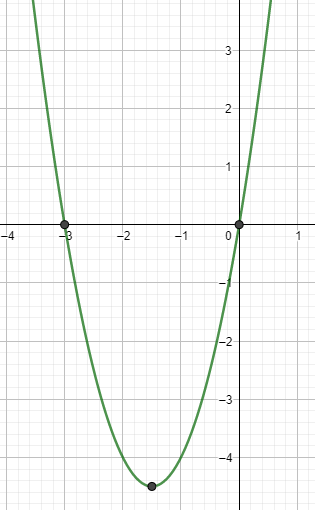
Der Scheitelpunkt der Parabel liegt zwischen den Nullstellen bei x = -1,5.
\(2\cdot (-1,5)^2+6\cdot (-1,5)=-4,5\)
Wenn du jetzt noch den Scheitelpunkt einträgst, solltest du die Parabel skizzieren können.
Gruß, Silvia