Bestimme die ganzrationale Funktion

Question

Aufgabe:

Bestimme eine ganzrationale Funktion f, die einen Hochpunkt bei (1|0) und einen Tiefpunkt bei (-1|0) hat.

Problem/Ansatz:

Mein Ansatz ist, dass es eine Funktion fünften grades ist und ein minus als Vorzeichen hat. Ich komm aber einfach nicht weiter, weil mit Bedingungen kann ich ja auch nicht weiter kommen.

Kann mir da jemand bitte helfen?

Answer 1

Bestimme eine ganzrationale Funktion f, die einen Hochpunkt bei (1|0) und einen Tiefpunkt bei (-1|0) hat.

Hallo,

ich bin mit einem Funktionsplotter an die Aufgabe herangegangen.

Bei +1 und -1 liegen doppelte Nullstellen vor. Deshalb ist (x-1)^2•(x+1)^2 ein interessanter Kandidat. Allerdings hat die Funktion dann beide Male ein Minimum, also einen Tiefpunkt.

Nun soll bei (1|0) aber ein Hochpunkt liegen. Daher habe ich meinen Term noch mit x multipliziert und schließlich noch mit (-1).

f(x)=-x(x-1)^2•(x+1)^2

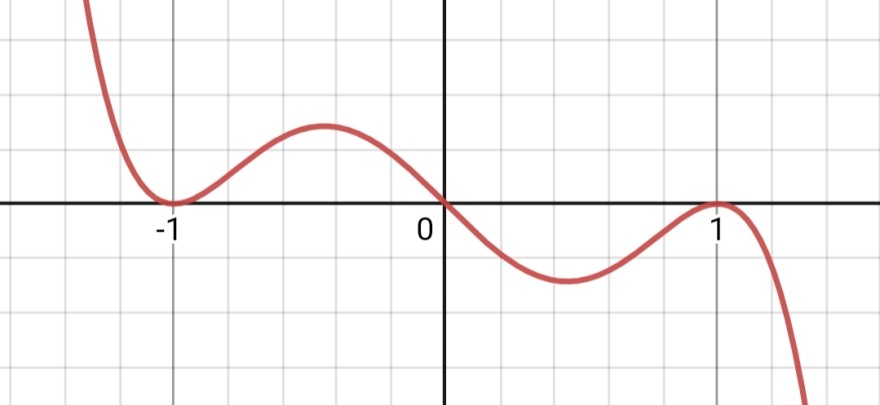
Wie kannst du das rechnerisch lösen?

Die Informationen lassen auf eine zum Ursprung punktsymmetrische Funktion schließen.

f(x)=ax^5+bx^3+cx

f'(x)=5ax^4+3bx^2+c

f"(x)=20ax^3+6bx

f(1)=0=a+b+c  (*)

f'(1)=0= 5a+3b+c  (**)

f"(1)<0 → 20a+6b<0  (***)

(**)-(*) → 4a+2b=0 → b=-2a

In (***) einsetzen: 8a<0 bzw. a<0

Nun gibt es beliebig viele Lösungen. Ich setze daher a=-1.

--> b=2, c=-1

f(x)=-x^5+2x^3-x

Das entspricht genau meiner oben bestimmten Funktion.

:-)

Comments

Vielen Dank!

Answer 2

Du hast 4 Infos:

f(1)=0

f(-1)= 0

f '(1) = 0

f '(-1) = 0

f(x) = ax^3+bx^2+cx+ d

Comments

Das kann nicht sein; denn die ersten 4 Bedingungen, die du

hingeschrieben hast, besagen, dass 1 und -1 mindestens

doppelte Nullstellen sind, d.h.

\(f(x)=(x+1)^2(x-1)^2\cdot g(x)\) sein muss.

Ah, sehe gerade, dass MontyPython bereits einen

Treffer gelandet hat.

---

Der Fragesteller geht bereits von Grad 5 aus.

Wenn man sich die Bedingungen graphisch skizziert, erkennt man, dass es mindestens 4 Extrema geben muss, also Grad 5.