Der Graph einer Polynomfunktion f dritten Grades besitzt an der Stelle - 1 eine Wendestelle

Question

Aufgabe:

Der Graph einer Polynomfunktion f dritten Grades besitzt an der Stelle - 1 eine Wendestelle
Die Steigung der Tangente im Wendepunkt beträgt 1,5. Der Punkt P= (-2|-2) ist ein
Tiefpunkt. Bestimme die Funktionsgleichung von f.

Problem/Ansatz

Was genau macht man wenn in der angabe die steigung der tangente im wendepunkt angegeben ist?

Answer 1

Hallo,

Steigung = 1. Ableitung, und dann weißt du f'(-1) = 1,5.

Gruß, Silvia

Schreibe bitte die Koordinaten von P noch richtig hin.

Comments

Dankeschöm Icch habe es verstanden: Und was macht man wenn besipilesweise steht Polynymfunktion: dritten Grades besitzt an der Stelle - 1 eine Wendestelle
mit der Wendetangente t: 6x + 3 y =-5.  Wie muss ich bei der Wendetangente vorgehen?

---

Stelle um:

6x+3y= -5

3y = -5-6x

y= -5/3 -2x

d.h. die Tangente hat die Steigung m= -2

f '(-1) = -2

Answer 2

f(x) = ax^3+bx^2+cx+d

f '(x)= 3ax^2+2bx+c

f ''(x) = 6ax+2b

f(-21) = -2

f ''(-1)= 0

f '(-1) = 1,5

f '(-21) = 0

Answer 3

Hallo,

zum Vergleich:

\(f(x)=-0,5x^3-1,5x^2\)

Answer 4

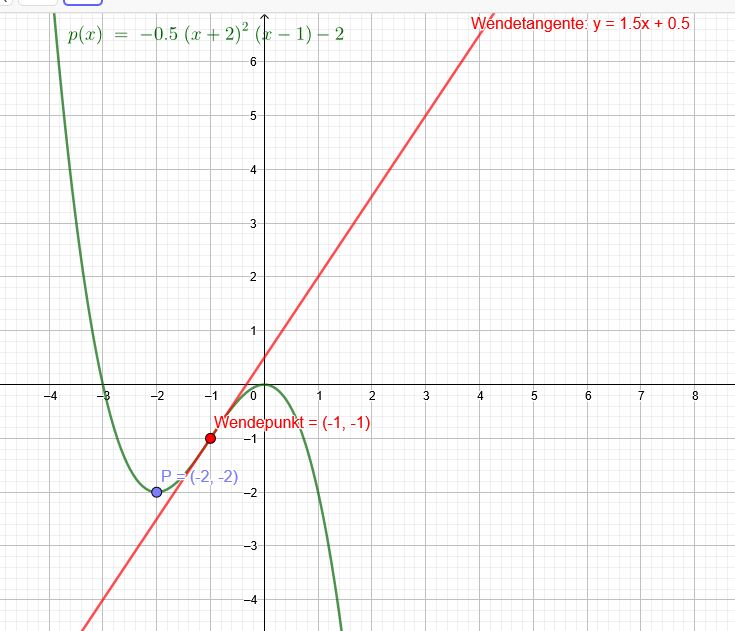
"Der Graph einer Polynomfunktion f dritten Grades besitzt an der Stelle \(x=- 1\) eine Wendestelle
Die Steigung der Tangente im Wendepunkt beträgt 1,5. Der Punkt \(P (-2|-2)\) ist ein
Tiefpunkt. Bestimme die Funktionsgleichung von f."

Ich verschiebe den Graph von f(x) um 2 Einheiten nach oben.

Tiefpunkt \(P (-2|-2)\)→ \(P´ (-2|0)\) ist eine doppelte Nullstelle.

\(f(x)=a*[(x+2)^2*(x-N)]\)

Steigung der Tangente im Wendepunkt:

\(f´(x)=a*[(2x+4)*(x-N)+(x+2)^2*1]\)

\(f´(-1)=a*[(2*(-1)+4)*(-1-N)+(-1+2)^2]\)

1.)  \(a*[2 *(-1-N)+1]=1,5\)

eine Wendestelle bei \(x=- 1\)

\(f´´(x)=a*[(2x-2N)+(2x+4)*1+(2x+4)]\)

\(f´´(-1)=a*[(2*(-1)-2N)+4*(-1)+8]\)

\(a*[(-2-2N)+4*(-1)+8]=0\)   →  \(N=1\)     \(a*[2 *(-1-1)+1]=1,5\)     \(a=-0,5\)

\(f(x)=-0,5*(x+2)^2*(x-1)]\)

Nun 2 Einheiten nach unten:

\(p(x)=-0,5*(x+2)^2*(x-1)-2\)