Aufgabe: (1+y(t)^2) * y(t)+4*t*y(t) = (1+t^2) ^(-2)
Problem/Ansatz:
ich komme nicht weiter beim Lösen folgender differentialgleichung.
Ich wollte die homogene Lösung durch trennung der Variablen erreichen und anschließend mit der Methode Variation der Konstanten die Allgemeine Lösung der dgl finden.
Leider komme ich beim Integrieren auf der rechten seite der gleichung nicht weiter.
Das t im Zähler stört mich irgendwie..
Habe ich ein Fehler gemacht?
Könnte jemand eventuell die Lösung der Dgl aufschreiben?
VIelen dank für jegliche hilfe..
Gruß
Frost 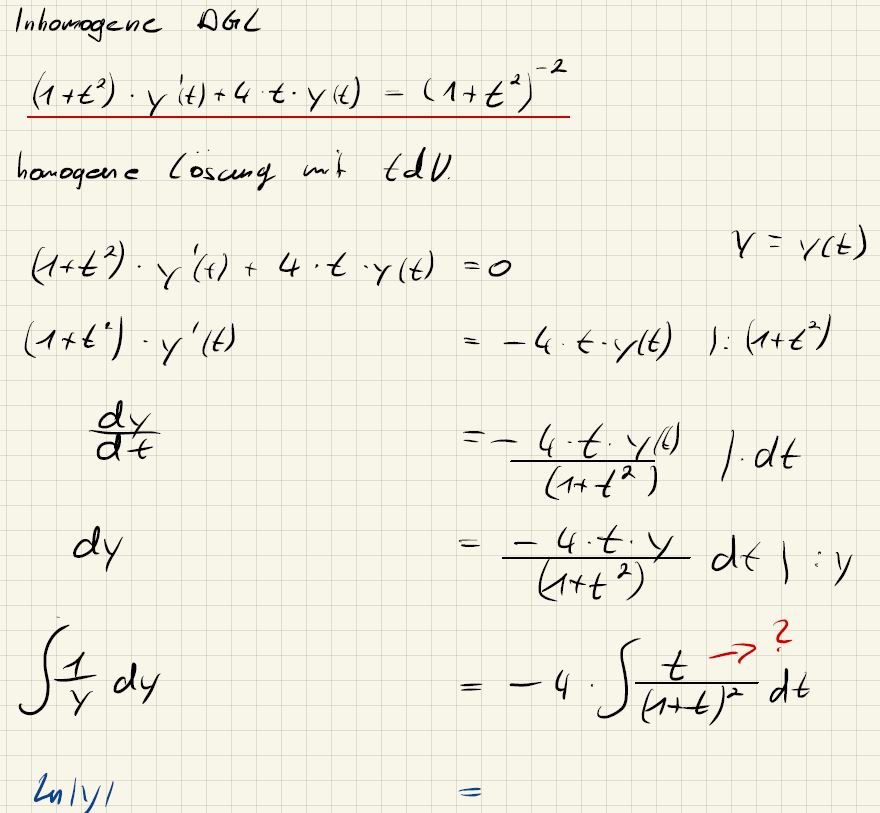
Text erkannt:
Inhomogene \( D G L \)
\( \underline{\left(1+t^{2}\right) \cdot y^{\prime}(t)+4 \cdot t \cdot y(t)=\left(1+t^{2}\right)^{-2}} \)
homogene losang mit tdV.
\( \begin{aligned} \left(1+t^{2}\right) \cdot y^{\prime}(t)+4 \cdot t \cdot y(t) & =0 \\ \left(1+t^{2}\right) \cdot y^{\prime}(t) \quad & y=y(t) \\ \frac{d y}{d t} & =-4 \cdot t \cdot y(t) \mid:\left(1+t^{2}\right) \\ & =-\frac{4 \cdot t \cdot y(t)}{\left(1+t^{2}\right)} \mid \cdot d t \\ & =\frac{-4 \cdot t \cdot y}{\left(1+t^{2}\right)} d t \mid: y \\ \int \frac{1}{y} d y & =-4 \cdot \int \frac{t \rightarrow t^{2}}{(1+t)^{2}} d t \\ & = \end{aligned} \)