Guten Abend,
ich habe wieder ein Umformungs-Problem:
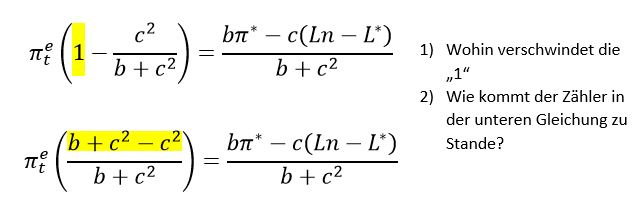
Text erkannt:
\( \begin{array}{l} \pi_{t}^{e}\left(1-\frac{c^{2}}{b+c^{2}}\right)=\frac{b \pi^{*}-c\left(\operatorname{Ln}-L^{*}\right)}{b+c^{2}} \\ \pi_{t}^{e}\left(\frac{b+c^{2}-c^{2}}{b+c^{2}}\right)=\frac{b \pi^{*}-c\left(\operatorname{Ln}-L^{*}\right)}{b+c^{2}} \end{array} \)
1) Wohin verschwindet die \( 1^{\prime \prime} \)
2) Wie kommt der Zähler in der unteren Gleichung zu Stande?
Danke vorab für eure Hilfe :) !
Abendliche Grüße vom Schreibtisch,
Daniel