Aufgabe:
Problem/Ansatz:
Text erkannt:
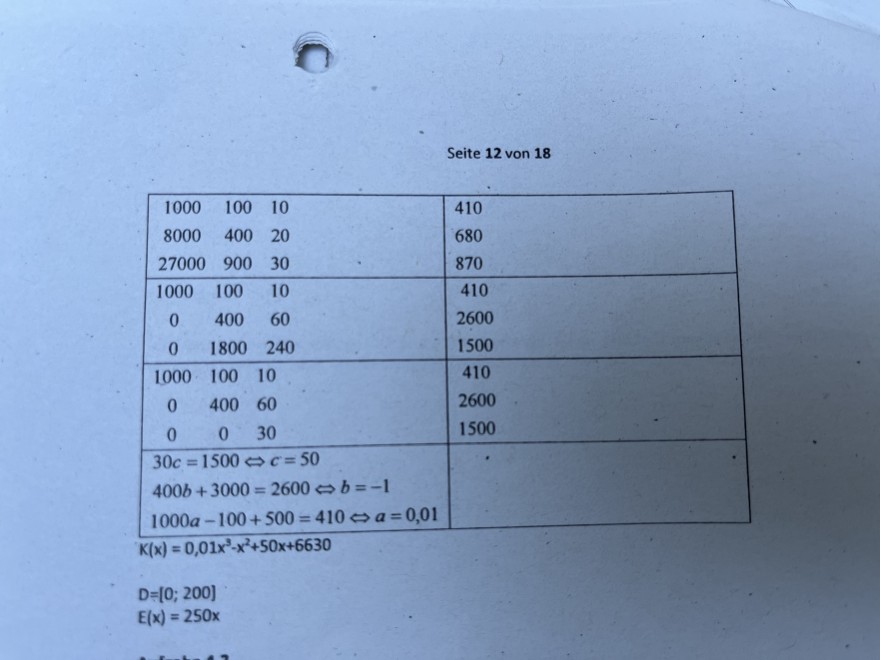
Seite 12 von 18

Text erkannt:
\( \begin{array}{l}\begin{array}{l}-8.000 .000 a-400.000 b-20.00 \\ 27.000 a+900 b+30 c=870\end{array} \\ 1000 a+100 b+10 c=4701.27 .000 \\ 0 a+900.000 b+60.000=2.600 .000 \\ 27.000 a+900 b+30 c=8 * 01 \cdot-1000 \\ \left.\begin{array}{c}27.000 .000 a+2700.000 b+270.000 c=14.070 .000 \\ 0 a+400.000 b+60.000=2.600 .000\end{array}\right]+ \\ -27.000 .000 a-900.000 b-30.000 \\ 0 a+400.000 b+60.000=2.600 .0001 .4 .800 .000 \\ 0 a+4.800 .000 b+240.000 c=-10.200 .0001 .-400.000 \\ 1000 a+400 b+-0 C=440 \\ \left.\begin{array}{l}0 a+00002700007,2 b+00000000071,08 c=0000020000004,68 \\ 0 a-00000500007,2 b-0000000000,6 c=-00000000004408\end{array}\right] \\ \mathrm{rooo} a+\operatorname{roob}+\mathrm{Coc}=4 \mathrm{ro} \\ 0 a+400.000 b+60.000=2.600 .000 \\ 0 a+0 b-8,52 c=0,61:-8,52 \\\end{array} \)
Text erkannt:
\( 8000 a+000+900 \)
\( 8.000 .000 a+800.000 b \)
a. mm m00a-400.000b
In der nachfolgenden Tabelle sind die Gesamtkosten \( \mathrm{K} \) in Geldeinheiten (GE) für x Mengeneinheiten (ME) angegeben.
\begin{tabular}{|c|c|c|c|c|c|}
\hline ME & \( \mathbf{x} \) & \( \mathbf{0} \) & \( \mathbf{1 0} \) & \( \mathbf{2 0} \) & \( \mathbf{3 0} \) \\
\hline \( \mathrm{GE} \) & \( \mathrm{K}(X) \) & 6630 & 7040 & 7310 & 7500 \\
\hline
\end{tabular}
Die Kapazitätsgrenze liegt bei \( 200 \mathrm{ME} \).
4.1 Ermitteln Sie die Parameter a, b c und \( d \) und weisen Sie nach, dass die Kostenfunktion durch \( K(x)=0,01 x^{3}-x^{2}+50 x+6630 \) beschrieben wird
Geben Sie den ökonomischen Definitionsbereich und die Erlösfunktion an.
4.2 Dem Geschäftsführer ist bekannt, dass bei einer Ausbringungsmenge von \( 30 \mathrm{ME} \)
Hey das ist die Frage Stellung. Ich habe die Aufgabe gelöst aber die ist ab der dritten Schritt bei mir falsch kann mir bitte einer helfen ich rechne die ganze Zeit nochmal aber ich bekomme nicht die Zahlen aus der Lösung