Trigonometrische Gleichung Winkeln herausfinden?

Question

Aufgabe:

Wenn ich von Cos einen Winkel weiß, wie bekomme ich die anderen Winkel?

Text erkannt:

\( \cos (3 x)=0,7 \)
Intervall 0 bis 360 Grad
\( \begin{array}{l} 3 x=u \\ \arccos (0,7)=u \\ \mathrm{u}=45,572 / 3 \\ =15,190 \mathrm{Grad} \end{array} \)

Problem/Ansatz:

…

Answer 1

Das mit dem u ist schon ein guter Ansatz! Du substituierst das was im cos drin steht mit u, berechnest u mit dem arccos und musst aber anschließend die Resubstitution machen, um das x zu erhalten! Pro Periode gibt es meist zwei Lösungen (Ausnahme cos(u) = 1). Um auf das zweite u zu kommen, kannst du entweder den Einheitskreis verwenden oder alternativ eine Zeichnung der Standard Kosinusfunktion. Mit dem zweiten u musst du auch die Resubstitution machen. Um nun auf alle Lösungen zu kommen, addierst du zu beiden x das k-fache der Periodenlänge (k ist eine ganze Zahl).

Auf dieser Wissenskarte findest du unten super ausführlich erklärte Beispiele für unterschiedlich komplexe trigonometrische Gleichungen.

Answer 2

cos(3·x) = 0.7

3·x = arccos(0.7)

x = arccos(0.7) / 3

x = 15.1909987°

Das ist also x und nicht u wie du geschrieben hast. Außerdem verstehe ich nicht wo du genau Probleme hast, außer das du nicht in der Lage bist es ordentlich zu notieren.

Comments

Wie rechne ich die anderen (restlichen) Lösungen

---

Wie rechne ich die anderen (restlichen) Lösungen

'rechnen' besser gar nicht, sondern sich eine Skizze vom Einheitskreis machen. Jeder Winkel im Einheitskreis, dessen Schenkel vom Ursprung \(O\) zu einem der Schnittpunkte der Vertikalen \(x=0,7\) mit dem Einheitskreis verläuft, hat den Cosinus von \(0,7\):

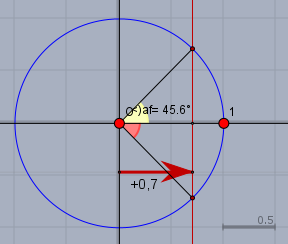
Wenn also der eine Winkel (gelb) den Wert von \(\approx 45,6°\) hat, so muss der andere (der rote) zwangsläufig \(\approx -45,6°\) groß sein. Und da die Winkel in Bereich von \([0\dots 360°)\) liegen sollen, so addiere nochmal \(360°\).$$\implies u_2 \approx 360° - 45,6°=314,4° \implies x_2 \approx 104,8°$$In Deinem konkreten Fall mit der Vorgabe (ist das so?)$$u=3x \quad x \in[0°\dots 360°)$$gibt es noch weitere Lösungen$$3x_3 \approx 2\cdot 360° - 45,6° \implies x_3 \approx 242,2° \\ 3x_4 \approx 3\cdot 360° - 45,6° \implies x_4 \approx 344,8°\\ 3x_5 \approx 360° + 45,6° \implies x_5 \approx 135,2° \\ 3x_6 \approx 2\cdot 360° + 45,6° \implies x_6 \approx 255,2°$$

---

arccos(0.7) ist nur ein Winkel an dem der Cosinus den Wert von 0.7 hat. Eine weitere Lösung ist -arccos(0.7), wie du der Skizze von Werner-Salomon entnehmen kannst.

Ebenso alle Winkel, die sich um eine Periode von den zwei Grundlösungen unterscheiden.

Answer 3

Der cos ist positiv im 1. und 4. Quadranten.

phi= 15,19 v phi= 360°-15,19 = 344,81°