" Bestimmen Sie die Koeffizienten b und c in der folgenden Gleichung so , dass das Polynom \(y= -0,5x^3 +bx^2+cx +2\) im Punkt \(E(2|-4)\) einen Extremwert hat. Bestimmen Sie den zweiten Extremwert."
\(y= -0,5x^3 +bx^2 +cx +2\)
\(E(2|-4)\):
\(y(2)= -0,5*2^3 +b*2^2 +c*2 +2\)
\( -4+4b +2c +2=-4\) → \( 2b +c +1=0\) →
1.)
\( c =-1-2b\)
\(y´= -1,5x^2 +2bx +c\)
\(y´(2)= -1,5*2^2 +2b*2 +c\)
\( -6+4b +c=0\)
2.)
\( c=6-4b\)
\( -1-2b=6-4b\)→\( b=3,5\) \( c=6-4*3,5\) \( c=-8\)
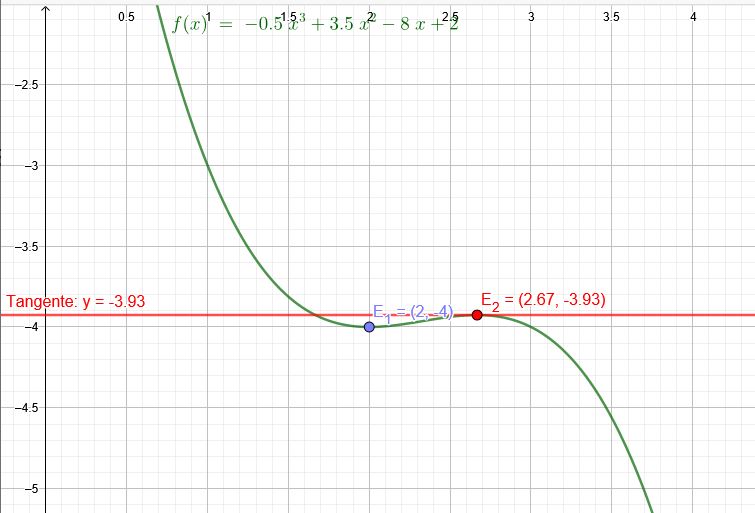
\(y= -0,5x^3 +3,5x^2 -8x +2\)
\(y´= -1,5x^2+7x -8\)
\( -1,5x^2+7x -8=0\)
\( x_1=2\) \( y_1=-4\)
\( x_2=\frac{8}{3}\) \( y_2=-0,5*(\frac{8}{3})^3 +3,5*(\frac{8}{3})^2 -8*\frac{8}{3} +2=-\frac{106}{27}\)