Aufgabe:
In einem Labor werden u. a. Bakterien untersucht. In der Petrischale vermehren sie sich. Dieser Vorgang wird in der untenstehenden Grafik dargestellt.
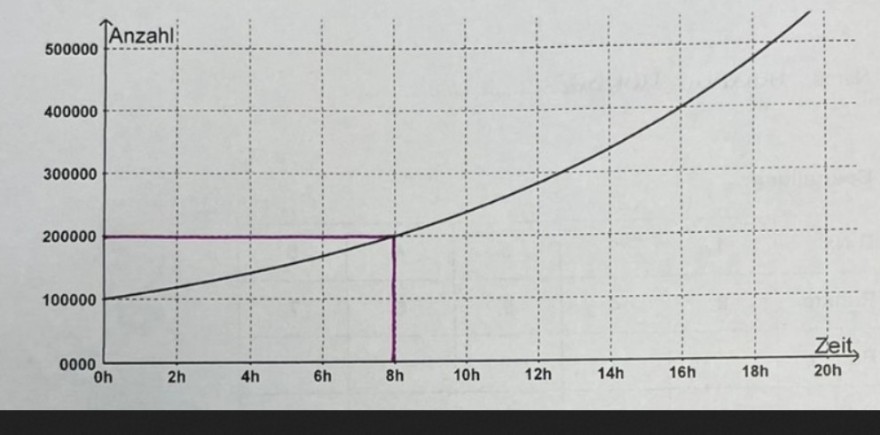
1.2. Geben Sie eine Gleichung an, welche die Anzahl der Bakterien nach \( \mathrm{t} \) Stunden angibt, wenn zu Beginn 120000 Bakterien vorhanden sind.
1.3. Berechnen Sie nachvollziehbar, wie lange es dauert, bis mehr als eine Million Bakterien vorhanden sind.
Problem/Ansatz:
1.2.
Wachstumsfaktor a ist gesucht also:
2=a8
a=1,09051
Die Funktion lautet also so: 120*1,09051t
1.3.
10000=120*1,09051t
t=51,04535 Stunden
Kann mir jemand sagen, ob das stimmt?