Bestimmen Sie einen Wert von k , so dass der Graph von f_{k} durch (2|3) verläuft.

Question

Text erkannt:

Pflichtaufgabe: Teil 2 - Aufgabe 1 - zum Themenbereich Analysis
Funktionsschar
Für jedes \( k \in \mathbb{R} \) mit \( k>0 \) ist die in \( \mathbb{R} \) definierte Funktion \( f_{k} \) gegeben durch
\( f_{k}(x)=-\frac{1}{4} x^{2}+k^{2} \)
a Beschreiben Sie den Einfluss des Parameters \( k \) auf den Graphen von \( \mathrm{f}_{\mathrm{k}} \). Bestimmen Sie einen Wert von \( k \), so dass der Graph von \( f_{k} \) durch (2|3) verläuft.
b Die zur x-Achse parallele Gerade mit dem y-Achsenabschnitt \( \frac{k^{2}}{2} \) schneidet den Graphen von \( \mathrm{f}_{\mathrm{k}} \) an zwei Stellen.
Berechnen Sie diese beiden Schnittstellen in Abhängigkeit von k.

Aufgabe:

Ich komme leider nicht bei Aufgabe b weiter können Sie mir bitte helfen

Ich habe wirklich versucht alleine die Aufgabe zu berechnen

Bitte Schritt für Schritt

Problem/Ansatz:

Das ist ja meine Rechnung aber irgendwie komme ich nicht weiter ?

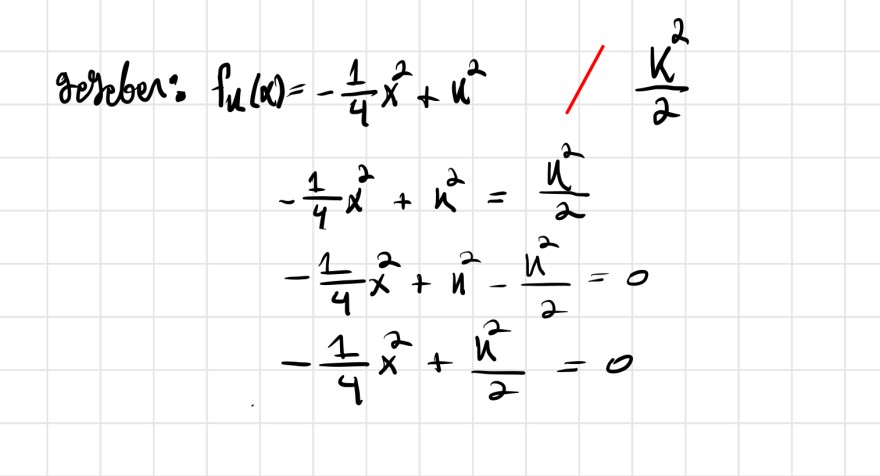
Text erkannt:

Getcber: \( \begin{aligned} f_{u}(x) & =-\frac{1}{4} x^{2}+u^{2} / \frac{k^{2}}{2} \\ & -\frac{1}{4} x^{2}+x^{2}=\frac{u^{2}}{2} \\ & -\frac{1}{4} x^{2}+u^{2}-\frac{u^{2}}{2}=0 \\ & -\frac{1}{4} x^{2}+\frac{u^{2}}{2}=0\end{aligned} \)

Answer 1

Aloha :)

Du hast bei deiner Rechung nicht ausgenutzt, dass der Graph durch den Punkt \((2|3)\) gehen soll. Das heißt nämlich, dass \(f_k(2)=3\) sein soll.$$f_k(2)=3\quad\bigg|\text{Funktionsterm eintragen}$$$$-\frac14\cdot2^2+k^2=3\quad\bigg|\text{Links das Produkt ausrechnen}$$$$-1+k^2=3\quad\big|+1$$$$k^2=4\quad\big|\sqrt{\cdots}$$$$k=\pm2$$Da jedoch nur \(k>0\) zugelassen ist, lautet die Lösung \(\pink{k=2}\).

Beim Teil (b) musst du die folgende Gleichung lösen:$$f_k(x)=\frac{k^2}{2}\quad\bigg|\text{Funktionsterm eintragen}$$$$-\frac14x^2+k^2=\frac{k^2}{2}\quad\bigg|-k^2$$$$-\frac14x^2=-\frac{k^2}{2}\quad\bigg|\cdot(-4)$$$$x^2=2k^2\quad\big|\sqrt{\cdots}$$$$x=\pm\sqrt{2k^2}=\pm\sqrt2\,k$$

Answer 2

Hallo

du bist doch fast fertig?

da steht doch fast x^2/4=k^2/2 also x^2=2k^2 und daraus die 2 wurzeln sind die Schnittstellen, die natürlich von k abhängen.

Gruß lul