Aufgabe:
Berechnung des Ellipsenumfanges, mit Kreischarakter bei ß=pi/4, über das Integral der Krümmungen
Problem/Ansatz:
Das Integral der Krümmung einer Ellipse mit a=8 und b=5 ist gleich dem Integral der Krümmung eines Kreises mit r=8!
Kreis: y^2+x^2=64 y=(64-x^2)^(1/2) y'=-x/(64-x^2)^(1/2) y''=-64/(64-x^2)^(3/2) Krümmung k=y''/(1+(y')^2)^(3/2) Das Integral der Krümmung von 0 bis 8 ergibt: -1 (.....im Viertelkreis)
Ellipse a=8,b=5 y^2/b^2+x^2/a^2=1 y=5*(1-x^2/64)^(1/2) y'=-5x/(8*(64-x^2)^(1/2)) y''=-40/(64-x^2)^(3/2) Krümmung k=.....
Das Integral der Krümmung von 0 bis 8 ergibt: -1 (.....Viertelellipse)
Das Integral der Krümmung von 0 bis pi/4=-1/2= Integral der Krümmung von pi/4 bis pi/2, bei einer Ellipse,
(Kreischarakter!)
Kreis: in 8 Kreissektoren unterteilt, wie die Ellipse bei der Berechung es Integrals der Krümmung, siehe darüber
1/8*U/S U=Kreisumfang=2*pi*r S ist die zugehörigen Kreissehnenlänge
r=5 1/8*U/S=3,927/3,827=1,02616 r=8 =6,283/6,123=1,02616
Diese beiden Eigenschaften, die Gleichheit des Integrals der Krümmungen und das gleiche Verhältnis des Kreisumfanges zur Sehnenlänge, ermöglichen es die Ellipse von 0 bis pi/4 und pi/4 bis pi/2, also eine Viertelellipse, wie einen Kreis bei der Berechnung des Umfanges zu behandeln!!!!!
http://www.wichmann.dashosting.de/mathematische%20Basteleien/Ellipse.html
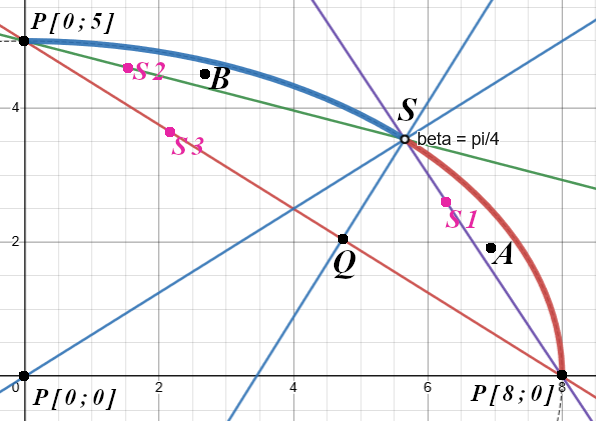
S1=4,2415027 S2=5,84333941
(5,84333941+4,2415027)*4*1,02616= 41,394646 bisher, näherungsweise: 41,38
Dezimalfehler in der Berechung führe ich auf ein ungenaues Rechnen bei S1 und S2 eventuell zurück.
Man sieht deutlich den Kreischarakter der Ellipse in den jeweiligen Bereichen.
Ich hoffe, dies ist alles richtig. Viele Grüße, Bert Wichmann!