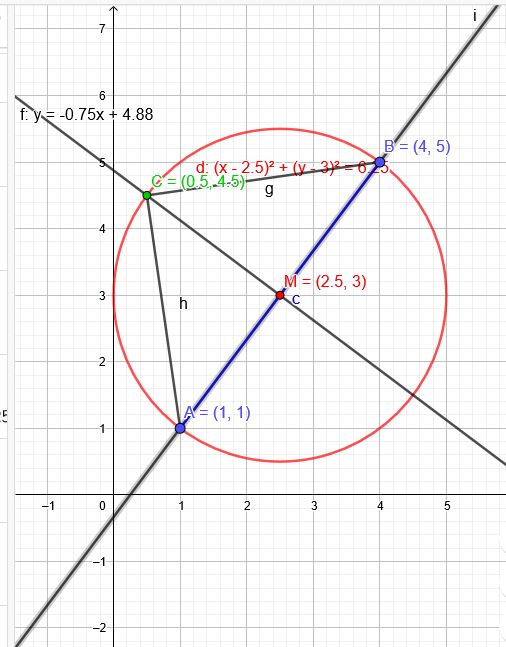
"Bestimmen Sie die Koordinaten eines Punktes C so, dass das Dreieck ABC mit \(A(1|1)\) und \(B(4|5)\) rechtwinklig und gleichschenklig ist."
Geradengleichung durch A und B:
Allgemein : \(\frac{y-y_1}{x-x_1}=\frac{y_2-y_1}{x_2-x_1}\)
\(\frac{y-1}{x-1}=\frac{5-1}{4-1}=\frac{4}{3}\)
Aufgelöst nach y:
\(y=\frac{4}{3}*x-\frac{1}{3}\) Die orthogonale Steigung beträgt: \(m=-\frac{3}{4}\)
Die Koordinaten des Mittelpunktes der Strecke (c) zwischen A und B:
\(M(\frac{1+4}{2}| \frac{1+5}{2})\)→ \(M(2,5| 3)\)
Länge der Strecke A B: \( c= \sqrt{(4-1)^2+(5-1)^2}=\sqrt{3^2+4^2}=5 \)
Der Radius des Kreises (Thaleskreis) um M ist \(r=2,5\)
Allgemeine Kreisformel: \( (x-x_M)^2+(y-y_m)^2=r^2\)
\( (x-2,5)^2+(y-3)^2=6,25\)
Die orthogonale Gerade durch M:
Allgemeine Punkt-Steigungsformel einer Geraden:
\(\frac{y-y_1}{x-x_1}=m\)
\(\frac{y-3}{x-2,5}=-\frac{3}{4}\)
Aufgelöst nach y: \(y=-\frac{3}{4}*x+4,88\)
Diese Gerade schneidet nun den Thales Kreis in C.
\( (x-2,5)^2+(-\frac{3}{4}*x+4,88-3)^2=6,25\)
...
\(C(0,5|4,5)\)
Da die Punkte A, B und C entgegengesetzt dem Uhrzeigersinn angeordnet sind, entfällt der 2. Punkt C.