Berechnen Sie die Fensterhöhe

Question

Aufgabe: Berechnen Sie die Fensterhöhe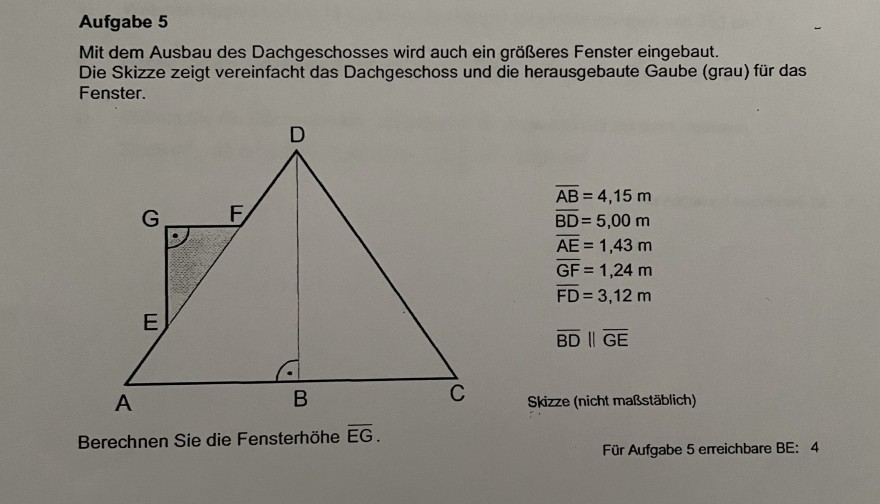

Text erkannt:

Aufgabe 5
Mit dem Ausbau des Dachgeschosses wird auch ein größeres Fenster eingebaut. Die Skizze zeigt vereinfacht das Dachgeschoss und die herausgebaute Gaube (grau) für das Fenster.
\( \begin{array}{l} \overline{\mathrm{AB}}=4,15 \mathrm{~m} \\ \overline{\mathrm{BD}}=5,00 \mathrm{~m} \\ \overline{\mathrm{AE}}=1,43 \mathrm{~m} \\ \overline{\mathrm{GF}}=1,24 \mathrm{~m} \\ \overline{\mathrm{FD}}=3,12 \mathrm{~m} \\ \overline{\mathrm{BD}} \| \overline{\mathrm{GE}} \end{array} \)
Skizze (nicht maßstäblich)
Berechnen Sie die Fensterhöhe \( \overline{\mathrm{EG}} \).
Für Aufgabe 5 erreichbare BE: 4

Problem/Ansatz: Können Sie mir hier weiterhelfen?

Answer 1

AD mit dem satz des Pythagoras ausrechen. Von AD die Strecken AE und FD abziehen, dann hast du EF. Jetzt wieder Pythagoras anwenden und du bekommst GE.

Answer 2

$$ (AB)^2+(BD)^2=(AD)^2$$

$$ EF=AD-(AE+FD)$$

$$ GE= \sqrt{(EF)^2-(GF)^2}$$

Comments

EF gibt es garnicht?

---

EF ist die Strecke vom Punkt E zum Punkt F. Das ist die Hypotenuse von dem Dreieck was du zur Beerechnung der Höhe brauchst.