Aufgabe: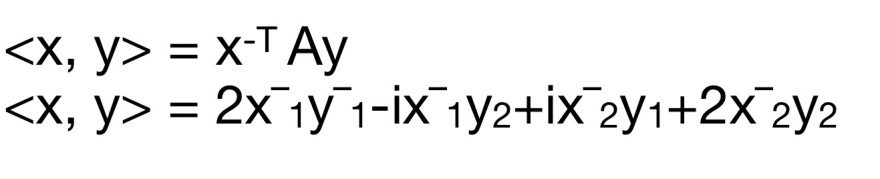
Text erkannt:
\( \begin{array}{l}<x, y>=x^{-\top} \mathrm{Ay} \\ <\mathrm{x}, \mathrm{y}>=2 \bar{x}^{-}{ }_{1}^{-y_{1}^{-}}-\mathrm{i} \mathrm{x}_{1}^{-}{ }_{1} \mathrm{y}_{2}+\mathrm{ix}_{2}^{-} \mathrm{y}_{1}+2 \mathrm{x}_{2}^{-} \mathrm{y}_{2}\end{array} \)
Die Striche sind jeweils x und y quer.
Problem/Ansatz:
Man soll hierbei feststellen, ob Bilinearformen, symmetrisch, difinitheit, Skalarprodukte, etc. vorliegen. Davon verstehe ich die Gegebenheiten. Allerdings habe ich große Probleme mit den Rechenregeln dieser Abbildungen, weshalb ich total auf dem Schlauch stehe. Wäre lieb, wenn mich jemand erleuchten könnte. Vielen Dank!